The complexity of a “simple” predator–prey system: non-trophic positive interactions generate unsuspected dynamics and dependencies

In natural ecosystems, many species engage simultaneously in both trophic and non-trophic interactions (NTIs), influencing each other's population growth and patterns of local coexistence. However, in coastal marine systems, where the larvae of most benthic adults disperse and frequently settle into populations distant from their origin, populations do not experience feedback from local reproduction. This implies an apparent decoupling between local dynamics and regional-scale dispersal processes. Here, we explore the consequences of positive NTIs for the coexistence and dynamics of a predator and its prey. Inspired by two species studied in the Chilean intertidal zone, we developed a predator–prey model in which the prey also facilitates the recruitment of and provides refuge to the predator, while larval subsidies externally control the population growth of both species. The predator–prey dynamic was simulated at different levels of species recruitment, with and without NTIs. Overall, NTIs led to density dependence of the predator on the prey, coupling their abundances across varying levels of larval subsidies. Furthermore, the impact of NTIs on predator abundance was non-additive, with the magnitude of these effects depending on recruitment rates. In addition to determining population growth, recruitment rates also modulate the extent to which the predator is facilitated by the prey. These results suggest that incorporating NTIs into dynamic models and ecological theory is necessary for a more complete understanding of the mechanisms of species coexistence and spatial variability. This knowledge is critical for understanding ecosystem responses to ongoing climate and global changes.

1 Introduction

At the core of natural communities, coexisting species engage in complex relationships that include trophic as well as non-trophic interactions, such as interference between predators or facilitation. These interactions determine whether species can fulfill their basic requirements and persist given environmental and biological constraints (Berlow et al., 2004; Kéfi et al., 2012; Stachowicz, 2001) and often act at the same time in natural settings. For example, a predator species might compete with another for prey while being facilitated by another species that provides refuges, often belonging to a lower trophic level, e.g., plants (Castilla and Luxoro, 1989; Kéfi et al., 2016; Navarrete and Castilla, 1988). These overlapping effects of interactions imply that even when a species is able to feed enough to meet its metabolic requirements, its persistence can depend on facilitative interactions with other species, which modulate assimilation or mortality rates (Kéfi et al., 2012). While significant theoretical and practical advances have been achieved by considering only a single type of species interaction at a time, such as predator–prey or plant–pollinator, it is clear that in real communities, species regularly engage in trophic and non-trophic interactions simultaneously (Kéfi et al., 2012; Miele et al., 2019; Sander et al., 2015).

Examples of pairs of species interacting simultaneously in multiple ways abound. For instance, many fish species consume kelp, which also serves as their habitat (Andrew and Jones, 1990; Jones, 1992; Pérez-Matus et al., 2022). Similarly, ungulates often find refuge by mixing in herds of other species, even while competing for the same food resources (Sinclair, 1985; Sinclair and Norton-Griffiths, 1982). In marine systems, certain crab species take refuge within mussel beds, which also constitute their main prey (Navarrete and Castilla, 1988; Wieters et al., 2009). Such complex relationships often involve “keystone” species that provide important habitat, such as trees, corals, mussels, or kelp (Bruno et al., 2003; Jones et al., 1997; McIntire and Fajardo, 2014; Timóteo et al., 2023). Network-level investigations have illustrated the importance of such multiplex interactions for community stability, diversity, and function (Kéfi et al., 2012; Miele et al., 2019; Gross, 2008; Mougi and Kondoh, 2012; Mougi, 2024; Lurgi et al., 2016). Despite this progress, we still lack a mechanistic understanding of how this overlap of different types of interactions shapes realized population dynamics, especially at the pairwise level.

We focus here on a pair of species for which at least two strong interactions have been identified experimentally, the mussel species Perumytilus purpuratus and one of its main predators, the crab Acanthocyclus hassleri. On top of their strong trophic interaction (Caro et al., 2008; Castilla and Luxoro, 1989; Navarrete and Castilla, 1988, 2003; Escobar et al., 2018), these species engage in other non-trophic interactions. In this case, mussels form beds with small cracks that facilitate the recruitment of crab larvae and provide refuge from predators to juveniles and adult crabs (Navarrete and Castilla, 1990; Wieters et al., 2009). Several laboratory and field manipulations and observations have quantified rates of crab predation on mussels (Castilla and Luxoro, 1989; Escobar et al., 2018; Navarrete and Castilla, 1988, 2003), as well as the recruitment facilitation for the crab by established mussel beds (Navarrete and Castilla, 1990; Navarrete et al., 2008) and refuge utilization and reduction in crab mortality thanks to refuges provided by mussels (Navarrete and Castilla, 1990; Wieters et al., 2009). This body of work highlights the complexity that emerges from what initially appears to be a “simple” predator–prey system, which makes it an ideal biological model to explore how these intricate local interactions (including predation, recruitment facilitation, and refuge provisioning) modulate local population dynamics.

The existence of non-trophic interactions occurring on a backdrop of trophic interactions may be particularly important in understanding ecological dynamics in open systems, such as the benthic–intertidal setting considered here. Most marine benthic species release gametes or larvae that are fertilized and develop in the water column for days to months, completing development before recruitment to adult populations. During this period, they are often dispersed by ocean currents until a suitable environment is found in which they can metamorphose, grow, and reproduce (Cowen and Sponaugle, 2009; Kingsford et al., 2002). This has important consequences for population dynamics. If a population is defined within a spatial scale smaller than the species dispersal capability, all the propagules produced at any given place could be transported away (Kinlan and Gaines, 2003; Lett et al., 2015; Ospina-Alvarez et al., 2018; Shanks et al., 2003). Consequently, there is little to no feedback to local populations from species reproduction (Gaines and Lafferty, 1995; Navarrete et al., 2010), and population replenishment primarily occurs through the arrival of new larvae from other geographical sites (Gaines and Roughgarden, 1985; Roughgarden et al., 1988). To what extent dispersal alters the outcome of local interspecific interactions, driving population dynamics and community patterns of diversity, is still a matter of research in ecology (Leibold et al., 2004; Navarrete et al., 2005).

Theoretical developments for such open systems have traditionally focused on the effects of dispersal between sites within metapopulation models (see Roughgarden and Iwasa, 1986; Roughgarden et al., 1988; and Aiken and Navarrete, 2011, for some examples in marine systems), and approaches that include interactions do so by modeling trophic interactions occurring at a single site within a food web, with a pool of immigrant individuals (Gaines and Lafferty, 1995; Wieters et al., 2008; Velazquez et al., 2005; Xing et al., 2016). Other works consider metacommunities with local interactions in which species either compete (Aiken and Navarrete, 2014; Amarasekare, 2003; Amarasekare and Nisbet, 2001; Levin, 1974; Leibold et al., 2004) or engage in predator–prey relationships (Caswell, 1978; Gaines and Lafferty, 1995; Han et al., 2019; Roughgarden et al., 1985), either in pairs or in tri-trophic food webs (as defined by Hastings and Powell, 1991). In all cases, these approaches only considered cases in which species pairs engage in a single type of interaction. For instance, in agreement with predictions of simple heuristic predator–prey models, Wieters et al. (2008) showed that the local abundance of different short-dispersal predators tracked the recruitment rates of the prey, while long-dispersal predators do not rely on prey population size or recruitment. Still, non-linear relationships exist between some of those open predators and open prey populations (Figs. 1–2 in Wieters et al., 2008). A more realistic understanding of complex ecological settings requires considering both trophic and non-trophic interactions to understand how they modulate the dynamics of open communities (Barner et al., 2016; Baskett and Salomon, 2010; Donohue et al., 2017; Gouhier et al., 2011; Gross, 2008; Kéfi et al., 2012).

To assess the effect of non-trophic interactions on the dynamics of an open community, we developed here a predator–prey open model that considers both the trophic and the non-trophic facilitative interactions between the mussel Perumytilus purpuratus and the predatory crab Acanthocyclus hassleri. We visualize the system as occurring over local scales that provide negligent feedback to future recruitment of new individuals, i.e., as completely open local populations. We used a numerical approach to explore the coexistence space, parametrized with experimentally derived data. Since previous open predator–prey models and field data showed that the abundance of the predator is independent of local prey recruitment or population size (Gaines and Lafferty, 1995; Wieters et al., 2008), we examined how this dependency changes across gradients of predator and prey recruitment when species also engage in non-trophic interactions (NTIs).

2 Methods

2.1 The ecological system

The mussel Perumytilus purpuratus (prey) and predator Acanthocyclus hassleri have larval stages that develop in the water column for periods of 14–20 and 20–30 d, respectively. Thus, over scales of hundreds of meters to a few kilometers, the arrival of new individuals can be considered independent of local abundance (Caro et al., 2010; Navarrete et al., 2010). The crabs recruit amongst mussels when mussels form a thick bed matrix (Navarrete et al., 2008), and as they grow, juveniles and adults build galleries underneath the mussel bed matrix (Castilla and Luxoro, 1989; Navarrete and Castilla, 1988). Observations and experimental data show that crab larvae prefer to settle in mussel beds over other microhabitats (Navarrete and Castilla, 1990; Navarrete et al., 2005, 2008). Adult alongshore abundances in the intertidal zone have been correlated with mesoscale oceanographic processes, which drive spatial variation in recruitment rates over scales of tens of kilometers (Navarrete et al., 2005, 2008). There is no linear or other simple relationship between mean mussel recruitment rate and adult abundances (mussel cover), nor is there one between crab recruitment and adult crab density across sites spread over 900 km (Wieters et al., 2008; Navarrete et al., 2008). Although adult crabs inhabit other microhabitats besides mussel beds, Wieters et al. (2009) showed that they choose mussel beds over other microhabitats, and Navarrete and Castilla (1990) showed that the galleries within the mussel bed protect crabs from visual predators (birds). Therefore, as expected, Navarrete et al. (2008) found that the density of crab predators was strongly and non-linearly related to mussel cover, increasing 2 to 5 times at sites where mussel cover surpassed approximately 60 % (Navarrete et al., 2008).

2.2 The trophic component of the predator–prey model

We used a dynamic, locally open predator–prey model in which the growth of the prey (V) and that of the predator (P) depend on the larval arrival from an external planktonic source; i.e., there is no feedback of local reproduction on population replenishment. This model captures the dynamics of populations where dispersal capabilities largely surpass the scale of local interactions and larval retention. The model is modified from Gaines and Lafferty (1995) and Wieters et al. (2008) to include space-limited recruitment for the prey and predator and a predator's functional response. Because they are open to recruitment from an external pool, the system exhibits local and global stability (Gaines and Lafferty, 1995; Velazquez et al., 2005), as long as there is an influx of individuals from the external source. Our analyses, therefore, focus on the effects of non-trophic interactions on the predator–prey state space and response to externally determined fluctuations in recruitment. The predator–prey model is given by

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}V}{\mathrm{d}t}}=s\left(A_V-W_{V}V\right)-m_{V}V-f\left(V\right)P,\text{(2)}& {\displaystyle }& {\displaystyle \frac{\mathrm{d}P}{\mathrm{d}t}}=c\left(A_P-W_{P}P\right)-m_{P}P,\end{array}$$

where s and c are arrival rates of prey and predator larvae, respectively, at a given site.

Larval arrival rates of the prey and predator are assumed to be independent and determined by their respective larval availabilities or larval pools at a given locality, L_V and L_P; thus

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }s=h{L}_V,\text{(4)}& {\displaystyle }& {\displaystyle }c=g{L}_P,\end{array}$$

where h and g are scaling constants that measure the fraction of those larvae that actually arrive at the local site, which is determined by physical processes and larval settlement affinities. The effective recruitment of prey and predators at the site will be given by how much space is available for settlement, which is given by the total space at a site (A_V,A_P) minus the space already occupied by settled individuals. The constants W_V and W_P are the average areas occupied by an individual prey and predator, respectively, and are linked to adult body size.

The function f(V) describes per capita predation rates through a generalized Holling functional response (Holling, 1959) of the following form:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }f\left(V\right)={\displaystyle \frac{\mathit{\alpha }{V}^b}{\mathrm{1}+\mathit{\alpha }\mathit{\lambda }{V}^b}},\end{array}$$

where α denotes the attack rate of the predator, λ denotes the handling time, and the exponent b determines the type of the functional response. m_V and m_P are the prey and predator density-independent mortality rates, respectively.

2.3 Inclusion of non-trophic interactions

We included the non-trophic interactions that characterize this predator–prey system by making selected parameters of the trophic model depend on prey density (Kéfi et al., 2012, 2016).

Recruitment facilitation. This type of NTI modifies flows across the system boundaries by affecting the arrival of new predators into the system. Since the total larval pool is determined by physical–biological processes external to the system, we assume that the presence of prey changes the base affinity of larvae for the local site, g in Eq. (4), to a larger affinity g^′, when most space is occupied by prey. Following field observations (Wieters et al., 2008; Navarrete et al., 2008), we made predator recruitment c depend non-linearly on prey density V:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }c=\left(g+\left(g^{\prime }-g\right){\displaystyle \frac{V^a}{V^a+V_{\mathrm{0}r}^a}}\right)L_P.\end{array}$$

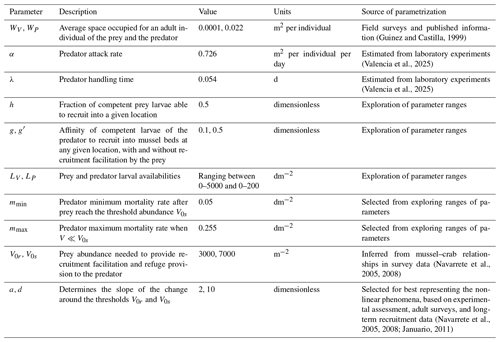
In this formulation, the parameter a determines the steepness of the increase in predator recruitment as a function of prey density V. A higher value of a results in a sharper transition in predator recruitment as prey density approaches the threshold value V_0r. This form implies that in the absence of prey, larval predator affinity for the site will be minimal and similar to that in the absence of NTI, which is c≈gL_P, as in the case of the purely trophic model. As prey density reaches values well above V_0r, predator larval affinity for the site increases to $c\approx g^{\prime }{L}_P$, leading to increased predator recruitment despite similar regional larval pools and available space (Fig. 1a).

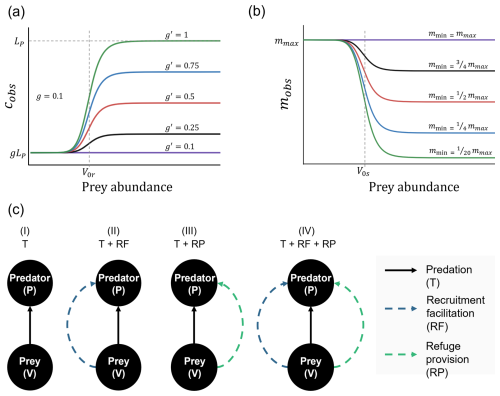
Figure 1 Sigmoid functions describing the dependence of (a) the predator recruitment rate and (b) the predator mortality rate on prey abundance while incorporating non-trophic interactions (NTIs): recruitment facilitation and refuge provision, respectively. (a) The fraction of larvae effectively recruited from a local larval pool (gL_P) increases as prey abundance approaches the threshold (V_0r). The total increase in recruitment depends on how much the base larval affinity (g) is elevated to a higher affinity (g^′) as prey occupy most of the available space. Thus, if $g^{\prime }=g$, recruitment facilitation is absent. (b) Predator mortality decreases from a maximum (m_max) to a minimum (m_min) as prey abundance approaches the threshold (V_0s). (c) Four modeled scenarios: (i) only the trophic interaction (T), (ii) trophic interaction and recruitment facilitation (T + RF), (iii) trophic interaction and refuge provision (T + RP), and (iv) trophic interaction combined with both NTIs (T + RF + RP).

Refuge provision. We considered refuge provision by the prey as a reduction in the predator mortality rates with prey density (Navarrete and Castilla, 1990). Again, we assume now that the predator mortality rate m_P is a non-linear function of prey density V:

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{m}_P=m_{\text{max}}-\left(m_{\text{max}}-m_{\text{min}}\right){\displaystyle \frac{V^d}{V^d+V_{\mathrm{0}s}^d}},\end{array}$$

where m_max is the maximum mortality rate; m_max≈m_P is reached at low prey densities, i.e., when predators cannot find refuge within the prey matrix; and m_min is the mortality rate reached at high prey densities. Thus, V_0s and d have the same role as before in determining the prey threshold value and the steepness of the function (Fig. 1b).

2.4 Parametrization

We parametrized the model based on field observations and experimental data (Table 1). The predator attack rate and handling time were estimated through functional response experiments (Fig. A1). The whole experimental procedure will be presented in a separate contribution. A type-II functional response (b=1) was selected as the best fit for experimental data using model selection and the Akaike information criterion (AIC). Maximum and minimum recruitment rate values were obtained from time series field data (Navarrete et al., 2005, 2008; Wieters et al., 2008). Plausible threshold densities V_0s and V_0r were inferred from published data that involve field surveys (see Navarrete et al., 2008). For the parameters that determine the steepness in the non-trophic interaction functions, a and d, we selected those that best represent the observed predator–prey adult abundance relationship in the natural system. In addition, we provide sensitivity analysis showing to what extent variation in these parameters could affect predator and prey abundances (Figs. A2 and A3).

(Guinez and Castilla, 1999)(Navarrete et al., 2005, 2008)(Navarrete et al., 2005, 2008; Januario, 2011)

Table 1 Parameters used. All the space units were converted to square meters (m²), and the time unit is days (d).

2.5 Simulations

We contrasted the dynamic behavior of four different models: (i) only trophic interaction (open predator–prey model), (ii) trophic interaction and recruitment facilitation, (iii) trophic interaction and refuge provision, and (iv) trophic with both non-trophic interactions (NTI) (Fig. 1c). This approach allowed us to compare the effect each NTI had relative to the fully trophic model across a range of prey and predator recruitment rates, s and c, and the mortality rate of the predator (m_P). For each model and parameter combination, we simulated the dynamics and retrieved the equilibrium state (Figs. A4 and A5). The ordinary differential equations were solved in R using the deSolve package (Soetaert et al., 2010).

To summarize how predator and prey abundances covaried depending on the subsidy of prey larvae, we considered the change in predator and prey abundances at equilibrium with recruitment of prey larvae, $\mathrm{d}{P}^{*}/\mathrm{d}s$ and $\mathrm{d}{V}^{*}/\mathrm{d}s$, and computed the ratio $\mathrm{d}{P}^{*}/\mathrm{d}{V}^{*}$ based on these two variables numerically, i.e., as $\mathrm{d}{P}^{*}/\mathrm{d}{V}^{*}=\frac{P^{*}\left(s\right)-P^{*}(s+\mathit{\delta }s)}{V^{*}\left(s\right)-V^{*}(s+\mathit{\delta }s)}$, where δs is a small change in the arrival rate of prey (set to 25). This ratio is equal to zero when an increase in the arrival of prey larvae produces no change in predator abundances at equilibrium. It is above zero when an increase in s produces a positive change in predator abundances, with higher values indicating a faster increase in predator relative to prey abundances. This ratio is expected to be non-negative, as an increase in prey subsidy should not lead to a decrease in predator or prey abundance. We computed this ratio for 100 values of s between 0 and 2500 $\mathrm{ind}.{\mathrm{d}}^{-\mathrm{1}}$ and varying c values between 0 and 3 $\mathrm{ind}.{\mathrm{d}}^{-\mathrm{1}}$.

3 Results

Our results indicate that non-trophic interactions (NTIs) imposed a qualitatively different behavior to the predator–prey open system by making the predator abundance depend on local prey recruitment rates. In contrast, this dependence was absent in the trophic model. Below, we describe first how recruitment facilitation and refuge provision shape population dynamics individually, then focus on their combined effects.

3.1 Recruitment facilitation and predator–prey dynamics

Focusing first on the increased predator recruitment by the prey, at any given site where prey was nearly absent (low values of hL_V, which yield V≪V_0r), the observed predator recruitment rate was similar to that in the absence of the non-trophic interaction (c≈gL_P; Fig. 2a1–a3). As prey recruitment increased, prey abundance approached and eventually surpassed V_0r, driving a non-linear increase in prey recruitment. Consequently, with predator larval availability unchanged, recruitment facilitation led to higher predator abundances than at the same sites without the NTI (Fig. 2c1–c3).

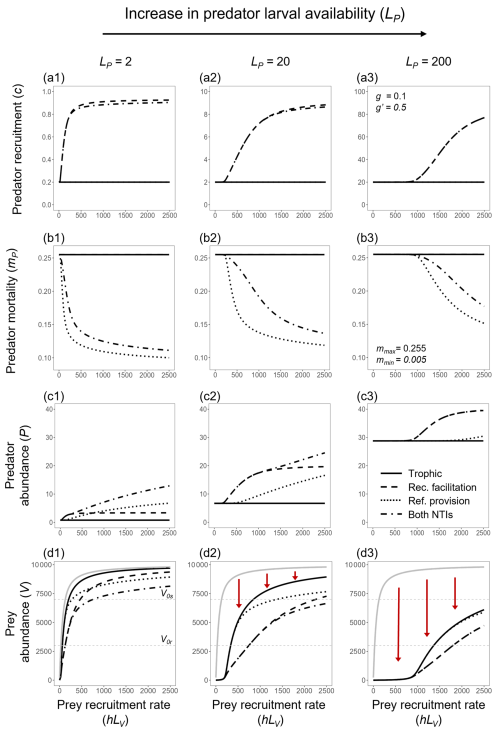
Figure 2 Variation in (a) the observed predator recruitment rate (c), (b) predator mortality (m_P), (c) predator abundance (P), and (d) prey abundance (V), across sites with different externally controlled prey recruitment rates (h_LV). Results are shown for four interaction scenarios: trophic interaction only (solid line), predation with recruitment facilitation (dashed line), predation with refuge provision (dotted line), and all interactions combined (dash-dotted line). Externally controlled predator larval availability (L_P) increases from left to right across the panels (L_P=2, L_P=20, and L_P=200). The solid gray line in the bottom panels (d1–d3) represents prey abundance in the absence of predators. Vertical red arrows in panels (d2) and (d3) indicate shifts in predator control over prey populations across different levels of prey recruitment.

Because predator abundance increased with the NTI, prey abundances were lower when the latter was included (compare solid and dashed lines in Fig. 2d1–d3). This effect intensified at sites with higher predator larval availability, requiring greater input of prey larvae to reach a given abundance, in contrast to the lower input needed when predator larval availability was reduced (i.e., compare levels of L_P in Fig. 2d1–d3). Consequently, stronger predator control increased the level of prey recruitment required to create habitat facilitation (the beneficial effect of the NTI) for predators.

The facilitation of predator recruitment implies that the rates of prey recruitment (hL_V), which are independent of ecological dynamics, will control predator abundance up to the point where prey abundance nearly reaches the entire available space ($V\approx A_V/W_V$) and predator recruitment reaches the maximum set by g^′L_P (Fig. 3b). Thereafter, further increases in prey recruitment do not alter prey abundance or predator recruitment, showing that the predator and prey abundances in this system are linked by the facilitation of predator recruitment rather than through prey consumption, as in the traditional closed predator–prey system.

Figure 3 Predator (P) and prey (V) abundances at a steady state across different combinations of predator larval availability (L_P; indicated by marker shapes) and prey recruitment rates (hL_V; color scale) under four different scenarios: (a) only trophic interaction, (b) predation with recruitment facilitation, (c) predation with refuge provision, and (d) all interactions combined. The vertical dashed line indicates the maximum number of prey individuals that can occupy a site (i.e., prey's carrying capacity), reached when $V=A_V/W_V$, which is determined by the total space available for prey (A_V) and the average space occupied by each prey individual (W_V). Similarly, the horizontal dashed line represents the maximum predator abundance, defined as $P=A_P/W_P$.

3.2 Refuge provision and predator–prey dynamics

Regarding the provision of refuge by the prey, our findings suggest that predator abundance was generally linked to prey abundance (and consequently their recruitment rate), with some notable differences compared to the other interaction. The predator mortality rate (m_P) followed a non-linear decrease with increasing prey recruitment rates, but the onset and steepness of this decline depended on the predator recruitment level (L_P; Fig. 2b1–b3). At low predator recruitment (L_P=2), m_P declines steeply, reaching m_min at relatively low prey recruitment rates (Fig. 2b1). As predator recruitment increases (L_P=20 and L_P=200), the decline in m_P becomes less steep and requires progressively higher prey recruitment rates to reach m_min (Fig. 2b2 and b3).

Moreover, at sites where predator larval availability was low and influx of larvae enabled prey abundance to approach V_0s, predator abundance increased almost linearly, rapidly exceeding the levels reached through the other non-trophic interaction (Fig. 2c1). However, in sites with higher levels of L_P, predator abundance never exceeded those levels reached due to recruitment facilitation (Fig. 2c2–c3).

Interestingly, the positive effect of prey on predators through the NTI accelerated, with a disproportionately positive effect at high prey abundances compared to low prey abundances (Fig. 3c). This contrasts with the other NTI (recruitment facilitation), which was saturated past a given prey abundance (Fig. 3b).

3.3 Combined effects of recruitment facilitation and refuge provision

Interesting patterns emerged when both NTIs were combined. First, along a gradient of the prey recruitment rate, the effects of both NTIs combined were identical to the case where only recruitment facilitation occurred. This remained true until prey recruitment became high enough to enable significant refuge provisioning (hL_V>250 and 1400 when L_P=2 and 20, respectively, as shown in Fig. 2). After this point, prey abundances were slightly lower when both NTIs were included than when only recruitment facilitation was present (Fig. 2c1–c2). However, under high predator recruitment (L_P=200), prey recruitment never reached the threshold required for refuge provisioning. In this case, despite being included in the model, refuge provision did not alter local abundances determined by recruitment facilitation (Fig. 2c3).

At any given site where prey reached V_0s, the predator population required prey recruitment that was approximately 3 times higher to achieve the same mortality rate compared to when only refuge provision was modeled (Fig. 2b1–b3). In other words, the reduction in predator mortality provided by refuges was lower when recruitment facilitation also occurred. Still, despite a potentially smaller effect overall, the inclusion of both NTIs remains beneficial to predators, whose abundances can reach levels beyond the maximum predator recruitment rate g^′L_P (Fig. 2c1–c2).

The addition of any form of NTI generates coupled predator–prey dynamics. However, the effects of refuge and recruitment facilitation are quite different, and these two forms of non-trophic facilitation are not additive in their impact on the predator–prey system. For instance, the provision of refuges can have stronger positive effects on predator abundance than recruitment facilitation at sites with low predator larval availability, but only where prey recruitment is high (Fig. 3d). The strength of the predator–prey dependency (coupled abundance dynamics) will occur over a much wider range of prey recruitment rates when there is facilitation of predator recruitment compared to when only refuge provision is included (compare Fig. 3b and c). In the latter case, refuge provisioning significantly affects predator abundances only at very high prey recruitment rates (Fig. 3c). Note that the maximum predator–prey dependency (steepness of curves in Fig. 3) occurs when both NTIs are included in the system (Fig. 3d), but, interestingly, the maximum predator and prey abundances barely surpass those observed when only recruitment facilitation is included (Fig. 3b).

3.4 NTI-mediated coupling of local abundances across larval subsidy gradients

When expressing the dependency between predator and prey abundances as the ratio of change in their abundances to the input of prey larvae, we first observed no change in relative predator abundances regardless of the level of the prey recruitment rate when no NTI was present (Fig. 4a). This shows that the arrival of new prey has no effect on predator abundance. Changes in this ratio were only observed when one or more NTIs were included, indicating that variations in prey abundance influenced predator abundance only in the presence of NTIs. However, this effect occurred in different regions of the recruitment parameter space. Under recruitment facilitation, predator abundance responded most strongly to prey larval influx at low to intermediate rates (200–1000), with the greatest impact occurring at relatively low influx (around 500, when predator recruitment was c=3; Fig. 4b). The effect of this NTI was saturated with the prey arrival rate (Fig. 3b), so an increase in prey did not result in an increase in predators past a certain arrival rate of prey (bottom-right purple area in Fig. 4b).

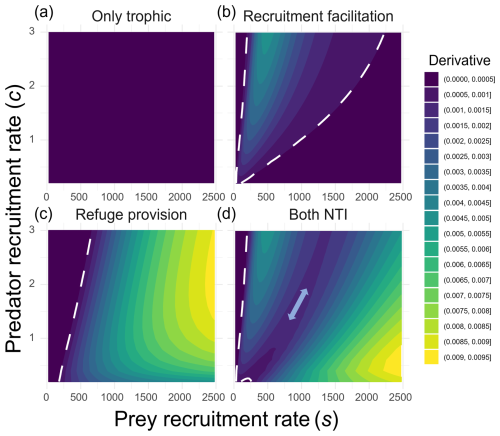
Figure 4 Strength of predator–prey coupling across gradients of predator recruitment rates (y axis) and prey recruitment rates (x axis) under four different scenarios: (a) only trophic interaction, (b) predation with recruitment facilitation, (c) predation with refuge provision, and (d) all interactions simultaneously. The coupling strength represents the extent to which predator abundance tracks changes in prey abundance. It was quantified as the numerical derivative of predator abundance with respect to prey abundance at equilibrium ($\mathrm{d}{P}^{*}/\mathrm{d}{V}^{*}$), calculated as $\mathrm{d}{P}^{*}/\mathrm{d}{V}^{*}=\frac{P^{*}\left(s\right)-P^{*}(s+\mathit{\delta }s)}{V^{*}\left(s\right)-V^{*}(s+\mathit{\delta }s)}$, where δs represents change in the prey larval arrival rate (set to 25). The dashed white line delineates regions where predator abundance remains unaffected by changes in prey recruitment (purple zone; uncoupled predator–prey dynamics) from those where predator abundance responds to prey larval recruitment (coupled predator–prey dynamics). The double-headed arrow in panel (d) highlights a region where the derivative approaches zero, indicating weak or independent predator–prey dynamics.

Conversely, the effect of refuge provision was not saturated but intensified with prey recruitment rates, while remaining almost negligible at low to intermediate values (purple area in Fig. 4c). As a result, when both NTIs were included, these patterns had beneficial effects on predators in two distinct regions of the parameter space (green and yellow areas in Fig. 4d). This left two areas where predator abundance remained mostly unaffected by prey recruitment: (1) at very low prey arrival rates and (2) at intermediate values (double-headed arrow in Fig. 4d).

4 Discussion

We have shown here that including any form of non-trophic interaction, recruitment, or refuge provision for an open predator–prey system triggers the emergence of strong dynamic dependencies between predator and prey abundances, which do not exist in a purely trophic model. The emergent dynamics resemble, in appearance, the dynamics of closed predator–prey systems, especially when the system is examined across gradients of prey recruitment rates, which are determined by externally controlled larval availability. The two NTIs had non-additive effects on predator and prey abundances, and the magnitude of the effects depended non-linearly on the rates of prey and predator recruitment. Below, we briefly discuss these findings.

A characteristic of open predator systems, in which predators and prey do not reproduce locally and new individuals arrive from external sources (e.g., larval pool), is the lack of correlation between predator–prey abundances across space or time and the strong dependence of predator abundance on its own fluctuating recruitment rates (Gaines and Lafferty, 1995; Velazquez et al., 2005; Wieters et al., 2008; Navarrete et al., 2010). Including a facilitative effect shifted the dynamics from being purely driven by the arrival of larvae to an interplay between regional and local processes. This is consistent with Gouhier et al. (2011), who, using a very different modeling approach, showed a similar shifting control in a competitive system when a subordinate species facilitates the recruitment of a dominant species. In our case, introducing any form of facilitation (NTI) forced previously unsuspected predator–prey dependencies that resulted not from changes in predator's fecundity but from prey-dependent alteration of effective predator recruitment and natural mortality rates. Commonly studied spatial correlations between prey and predators in marine systems (Witman et al., 2010; Navarrete and Manzur, 2008; Navarrete et al., 2008; Broitman et al., 2001; Caro et al., 2010; Menge et al., 2004) must therefore be interpreted with care, not only because of differences in life histories of the species examined (Wieters et al., 2008), but also because of the potential effect of non-trophic interactions between species.

The overall positive effect of both NTIs on predator abundance was expected. Empirical research on facilitation consistently shows that the presence of a facilitator species enhances the local density of the facilitated species (Bruno et al., 2003; Stachowicz, 2001). In our study, unexpectedly, the cost to the prey of facilitating its predator through an added NTI was rather marginal, with prey abundance experiencing only slight reductions even under varying levels of predator control. This suggests that predator facilitation by prey can easily emerge in natural communities, although such multiplex interactions are not widespread in marine ecosystems (Kéfi et al., 2015). In our context, the emergence of multiplex interactions may be enabled by the relatively weak per capita effect exerted by crabs on mussel populations, compared to other co-occurring intertidal predators (Navarrete and Castilla, 2003; Escobar et al., 2018). Predators with stronger control, such as the muricid gastropod Concholepas concholepas or the sea star Heliaster helianthus – both considered “keystone predators” in this system (Paine et al., 1985; Duran and Castilla, 1989; Navarrete and Castilla, 2003) – could significantly hinder mussel bed formation, preventing local prey populations from reaching the threshold abundance required to trigger NTIs and thereby limiting the prey coexistence space.

Notably, theoretical and empirical research on facilitation rarely involves density-dependent facilitative effects (but see Hart and Marshall, 2013, and Zhang and Tielbörger, 2020, for some exceptions). Instead, it often simply focuses on assessing the effect of the presence/absence of a facilitator species on the dynamics of another (Hart, 2023). However, the impact of the NTI relies not only on the presence of the benefactor but also on the density it might attain (Hart, 2023; Zhang and Tielbörger, 2020; Kéfi et al., 2012, 2016). In our system, incorporating prey abundance NTI thresholds generates a density dependence that modulates the population responses to environmental constraints. Externally driven prey recruitment determines not only prey growth but also the extent to which the predator benefits from the prey. Moreover, because each NTI had its strongest effect on opposite ends of the prey recruitment spectrum, the relative importance of these interactions for species dynamics varies across levels of prey larval variability. This constrains their impact on specific environmental settings, creating a dynamic landscape where different ecological mechanisms dominate depending on prey input rates. This implies, for example, that temporal fluctuations in prey recruitment could shift the balance between NTIs over time, potentially reshaping community structure in more complex ways than previously anticipated.

Recent investigations have shown that climate-induced shifts are driving significant changes in primary productivity and larval recruitment in coastal oceans, particularly throughout the Humboldt Upwelling Ecosystem (Aguirre et al., 2018; Navarrete et al., 2022; Weidberg et al., 2020). These changes may lead to profound alterations in the structure and composition of coastal marine communities, not only by disrupting the food supply for filter feeders (Navarrete et al., 2005; Menge et al., 2009) but also by influencing the intricate benthic–pelagic coupling mediated by the non-trophic interactions. Thus, unraveling these complex mechanisms is critical for improving multiplex network models that can provide qualitative predictions of ecosystem responses to global change (Kéfi et al., 2012, 2016). Such models represent a powerful tool for identifying species disproportionately impacted by the propagation of complex ecological interactions (Navarrete et al., 2023), enabling more informed and effective management decisions.

Several theoretical studies have shown that positive non-trophic interactions can yield destabilizing positive feedback loops and/or population cycles among interacting species (Baskett and Salomon, 2010; Gross, 2008; Gouhier et al., 2011). In our model system, populations approached a stable equilibrium (Fig. A4), even with one or both NTIs. This may be because the two facilitation mechanisms considered here are “unidirectional”, in the sense that the prey facilitates the predator, but the opposite is not true. Thus, despite the facilitative effect, there is no positive feedback. This is an important distinction compared to other systems, e.g., in plant–pollinator networks where both species benefit from the positive interaction and thus both benefit from an increase in the abundance of their partners. We suggest that there is no universal “destabilizing” effect of positive NTIs, as some authors have implied (see Neutel and Thorne, 2014, for an example showing that stability depends on the balance of feedbacks rather than on the mere presence of positive interactions). Moreover, we have parametrized numerical simulations using observed and well-documented interactions between a crab predator and its main mussel prey. Although we did not perform a complete sensitivity analysis of all parameters, we found that variations in non-empirically measured parameters had marginal impacts on the qualitative patterns observed, suggesting that our results are robust to small parameter uncertainties.

Understanding the mechanisms that modulate these dynamics and coexistence patterns in natural communities requires embracing the inherent complexity of species interactions, even in seemingly simple systems (Kéfi et al., 2012, 2015; Miele et al., 2019). Our work contributes to a better understanding of how trophic and positive non-trophic interactions (i.e., recruitment facilitation and refuge provision) in a predator–prey system interact with regional-scale processes, such as recruitment. Empirical approaches to validating theoretical findings often face logistical challenges, particularly in natural systems where large-scale processes like recruitment and dispersal complicate data collection and experimental manipulation. This highlights the value of “simple” local dynamic models, which distill complex interactions into testable hypotheses and provide valuable ecological insights (Gaines and Lafferty, 1995).

Like many models, ours assumes that all vital rates operate on the same temporal scale. Although this approach is common in population dynamics modeling, we recognize that it may oversimplify the inherent temporal asynchrony of biological processes in natural systems, potentially overlooking temporal mismatches that could influence population dynamics. Nevertheless, these models can integrate key ecological processes, such as dispersal-driven spatial heterogeneity in larval supply and density-dependent recruitment, and yield predictions that align well with observed biogeographical patterns – for example, the relationship between adult populations and larval recruits in mussels and barnacles (Caro et al., 2010; Navarrete et al., 2005; Wieters et al., 2008). Moving forward, integrating density-dependent processes and non-trophic interactions into these frameworks is essential for understanding non-linear responses and their potential propagation through trophic levels in multiplex networks.

Appendix A

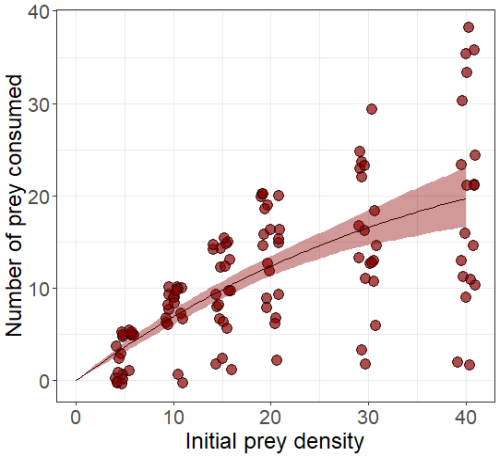
Figure A1 A functional response experiment was conducted at the Estación Costera de Investigaciones Marinas (Las Cruces, Chile) to estimate the predator's attack rate (α) and handling time (λ). Predators were individually placed in $\mathrm{10}\mathrm{cm}\times \mathrm{10}\mathrm{cm}\times \mathrm{10}\mathrm{cm}$ plastic aquaria (hereafter arenas), filled with filtered seawater, maintained with continuous aeration, and subjected to a 12 h : 12 h light–dark photoperiod. To standardize hunger levels, predators were starved for 3 d prior to the experiment. Prey were introduced into the arenas at one of six randomly assigned densities (5, 10, 15, 20, 30, or 40 individuals). After 48 h, the number of surviving prey in each arena was recorded. This figure presents the number of prey consumed at each prey density, based on the results of this experiment.

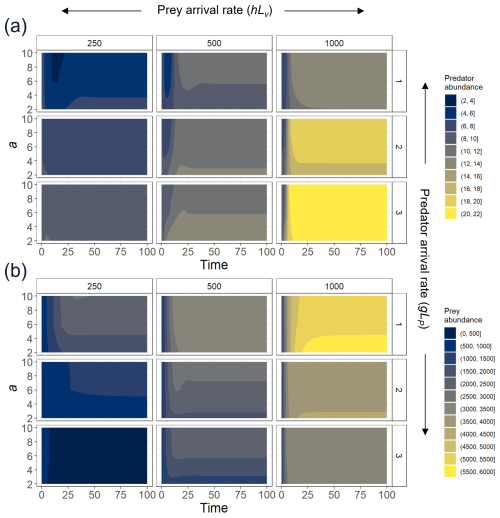
Figure A2 To explore the effect of the exponent a, we select three different levels of prey recruitment, hL_V (panels from left to right); three predator arrival rates, g^′L_P (panels from top to bottom); and values of a ranging between 2–10, and we solve the ordinary differential equations (ODEs; Eqs. 1 and 2) for the system in which predation and recruitment facilitation by the prey were modeled. Here, we present (a) predator and (b) prey abundances (color scale) over 100 time steps, time enough for the system to reach a steady state.

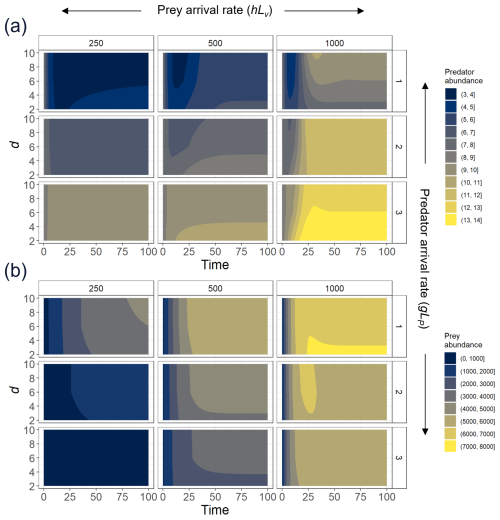
Figure A3 To explore the effect of the exponent d, we select three different levels of prey recruitment, hL_V (panels from left to right); three predator arrival rates, g^′L_P (panels from top to bottom); and values of d ranging between 2–10, and we solve the ODEs (Eqs. 1 and 2) for the system in which predation and recruitment facilitation by the prey were modeled. Here, we present (a) predator and (b) prey abundances (color scale) over 100 time steps, time enough for the system to reach a steady state.

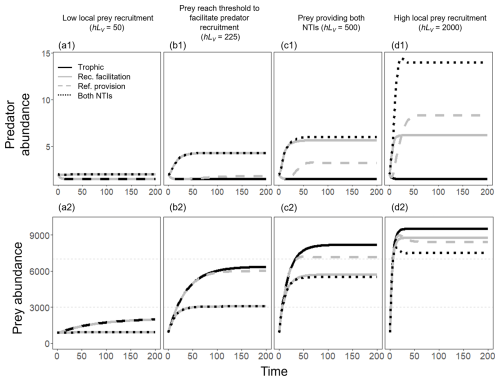
Figure A4 Population trajectories of the predator (a1–d1 panels) and the prey (a2–d2 panels) in four scenarios of prey recruitment – (a) low, (b) medium–low, (c) medium–high, and (d) high prey recruitment – when modeling only predation (solid black line), predation and recruitment facilitation (solid gray line), predation and refuge provision (dashed gray line), and all interactions at the time (dotted black line). Since the trajectories rapidly reached a steady state, we only show the first 200 time steps. We fixed L_P=2, g=0.1, $g^{\prime }=\mathrm{0.5}$, h=0.5, m_min=0.005, and m_max=0.255. When the refuge provision was not simulated, we assume m_P=m_max.

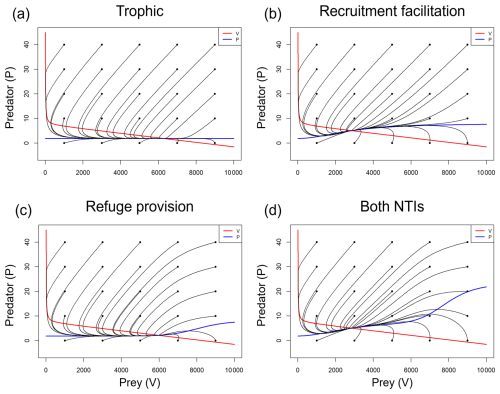
Figure A5 Phase portrait diagrams for the system when modeling (a) only predation, (b) predation and recruitment facilitation, (c) predation and refuge provision, and (d) all interactions simultaneously. The predator and prey nullclines are represented by blue and red lines, respectively. The black lines depict the system trajectories starting from different initial conditions (black dots), all converging in a stable equilibrium attractor, the intersection of the nullclines.