Model-based analysis of latent factors

The detection of community or population structure through analysis of explicit cause–effect modeling of given observations has received considerable attention. The complexity of the task is mirrored by the large number of existing approaches and methods, the applicability of which heavily depends on the design of efficient algorithms of data analysis. It is occasionally even difficult to disentangle concepts and algorithms. To add more clarity to this situation, the present paper focuses on elaborating the system analytic framework that probably encompasses most of the common concepts and approaches by classifying them as model-based analyses of latent factors. Problems concerning the efficiency of algorithms are not of primary concern here. In essence, the framework suggests an input–output model system in which the inputs are provided as latent model parameters and the output is specified by the observations. There are two types of model involved, one of which organizes the inputs by assigning combinations of potentially interacting factor levels to each observed object, while the other specifies the mechanisms by which these combinations are processed to yield the observations. It is demonstrated briefly how some of the most popular methods (Structure, BAPS, Geneland) fit into the framework and how they differ conceptually from each other. Attention is drawn to the need to formulate and assess qualification criteria by which the validity of the model can be judged. One probably indispensable criterion concerns the cause–effect character of the model-based approach and suggests that measures of association between assignments of factor levels and observations be considered together with maximization of their likelihoods (or posterior probabilities). In particular the likelihood criterion is difficult to realize with commonly used estimates based on Markov chain Monte Carlo (MCMC) algorithms. Generally applicable MCMC-based alternatives that allow for approximate employment of the primary qualification criterion and the implied model validation including further descriptors of model characteristics are suggested.

1 Introduction

Lately, methods of model-based ascertainment of hidden population substructure enjoy considerable popularity (most of which are variants of the approaches introduced in the papers of Pritchard et al., 2000; Corander et al., 2003; or Gouillot et al., 2005). The diversity of these methods, however, occasionally causes problems in comparing their results not just for reasons of the indeterminacy inherent in the complex approximation algorithms (mostly of the Markov chain Monte Carlo (MCMC) kind) applied to the estimation of multiple model parameters (for mathematical reasoning see, e.g., Roberts and Rosenthal, 2004). More basic problems may arise from the conceptual differences among the methods to the degree that their common features largely remain unrecognized. While for particular methods such as Structure (Pritchard et al., 2000) reviews that critically compare several variants (e.g., Porras-Hurtado et al., 2013) exist, attempts of comparing results obtainable from different methods are largely confined to simulation studies (see e.g., Neophytou, 2014).

To shed more light on general relations existing among approaches, an attempt is made in the present paper to outline the system analytic basis common to at least the most frequently applied methods and thus to enable clear distinction between the conclusions to be obtained from the different methods. Apparently, the above-cited methods were largely designed for the analysis of population structure that can be revealed for genetic characters. Extensions to ecological aspects of structure as realized, for example, in species communities or responses to environmental factors do however not seem to have been attempted, even though, as will be shown in this paper, they follow easily when generalizing the underlying reasoning (demonstrated in Sect. 3.1).

The farther-reaching interest in this topic comes from the common concern that inferences drawn from observations on collections of biological objects miss relevant information because the underlying forces and mechanisms are not traceable or escaped notice. This is especially disturbing if well-argued reasons or hypotheses that suggest the existence of special but untraceable cause–effect relations are at hand. Such concerns are almost routine in many studies of biological communities, for example, that are subject to variable environmental conditions, most of which escape proper identification but arguably exist (the above-cited work and its numerous applications are explicitly driven by this challenge).

To prevent possible misunderstanding, the problem addressed here is not one of descriptive statistics as known from the various kinds of statistical factor analysis, principal component analysis (PCA), data clustering, etc. (see, e.g., Reeves and Richards, 2009, who also make comparisons with model-based MCMC procedures), nor is it aimed at testing hypotheses on base populations inferred from samples as is familiar from inferential statistics. Instead, observations are considered as given, and questions are formulated as to potential cause–effect relations by which they can be explained. In essence, this amounts to the study of input–output model systems, in which the inputs are provided as latent model parameters and the output is specified by the observations. Model inputs are thus admissible only to the degree that they allow for realization of the observations. Borrowing from terminology of factor analysis, the input variables are referred to as (latent) factors. Being a variable, each factor can herewith realize several states called factor levels.

In such a system analytical context, the conjectured (hypothesized) forces are mirrored by the model mechanisms (the constructive specification of the system; for the system theoretic basis see, e.g., Mesarovic and Takahara, 1989). When population substructure is to be revealed on the basis of genetic traits, for example, these mechanisms are largely characterized by mating systems and migration patterns (which is central to the above-cited work on detecting population substructure for genetic traits) that operate within and among the potential subpopulations as factors.

Inference is then to be made on the factors and their levels, which may generate the observations and which meet certain qualification criteria. Especially in models involving probability laws, these criteria are mostly of a probabilistic nature and are related to the likelihood of the model parameters to reproduce the observation. In this context, calibration of model parameters so as to meet the qualification criteria (such as maximum likelihood or posterior probability) is thus of primary relevance. Low (maximum) evaluation scores, however, can give rise to the decision to reject the model because of insufficient qualification. This would be akin to testing the validity of the model (for an overview see, e.g., Burnham and Anderson, 2003), yet so far it does not seem to have played a central role in the analysis of latent forces.

The present paper concentrates on explicating the conceptual features of the above-sketched approach to modeling latent forces and demonstrates the integrating capacity of the concept by application to a small number of common methods. It does not expand on problems of numerical determination (estimation) of parameters since appropriate approximation algorithms (such as MCMC methods) are well established and efficient software exists. Yet, limitations to the conclusions to be drawn from application of MCMC algorithms will be outlined. In this context, descriptors of model qualification criteria will receive due consideration.

2 Model characteristics

A crucial feature of the present model is defined by the mode according to which the factors interact in generating the trait states of the observed objects. Modes of interaction include the absence of interaction in the sense that an observation is determined by a single factor only. Other modes of interaction are of an additive or multiplicative kind (or more generally based on separability of factor effects) as are familiar from statistical factor analysis. Yet, these modes of interaction are difficult or impossible to apply to qualitative or other more complex traits such as many genetic traits. The same problem of complexity arises when the species spectrum of a metacommunity is considered to result from the contributions of the individual communities acting as primary factors. Complexity may thus be a relevant issue for both traits and their causal factors.

It is therefore appropriate to proceed from a more general basis of inference as it is provided by the analysis of response functions. Here, each trait state is considered to be a response to factors that contribute effects that interact according to specified modes to yield the trait state. Two steps and associated sub-models can thus be distinguished in creating a response: the first (sub-model 1) determines individual factor contributions, and the second (sub-model 2) specifies the mode of interaction among the contributions.

The factor contributions include factor levels (e.g., in terms of effects on trait expression) as well as the degrees to which they participate in an object's trait expression. Since each observation is assumed to result solely from the contributions of the factors under consideration, it is meaningful to require that the factor participations of the contributions sum to 1. Factor contributions can therefore be represented as vectors with components corresponding to the factors, for which each component consists of two values, one reflecting the factor level or its effect and the other specifying the degree to which the factor contributes to or participates in trait expression.

In much of the above-cited work and its extensions concerned with genetic traits, an individual's observed genotype is conceived of resulting from a mating system that acts on a mixture of genes contributed by several populations. Hence, populations are the factors, the gene frequencies within a population define its factor level, and the mixture proportions specify the degrees to which the factors (populations) contribute to the gene pool from which the individual's genotype is formed. A contribution vector then appears as a thus structured gene pool. When populations are grouped into regions, for example, these regions may be conceived of as higher-order factors with levels specified by the individual populations. In other words, factor levels can themselves function as factors, by which a hierarchy of (higher-order) factors that may or may not explicitly appear in the factor contributions would result.

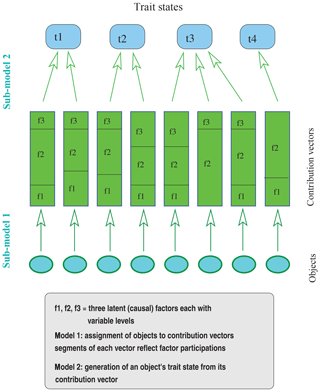
Figure 1 Illustration of the constituents involved in modeling the effect of latent factors on the trait expressions of a set of objects (note that assignment of two objects to the same contribution vector is not required to always generate the same trait state – as illustrated for the middle two objects).

Given these explanations, the observed collection of objects is conceived to result from an assignment of objects to contribution vectors (sub-model 1), which is followed by the generation of trait states from the contribution vectors (sub-model 2). Apparently, this approach considers the objects of the observed collection as entities that can be assigned contribution vectors, which in turn determine the entities' trait states (for an illustration see Fig. 1). Within each assignment, sub-model 1 can determine in various ways how factors and their levels are distributed over objects. For example, the level of a factor may not be allowed to vary among the contribution vectors of an assignment. When factors indicate origin as is the case in studies of common descent, this condition is mandatory. Other relationships among contribution vectors determined by sub-model 1 could be formulated in general terms of correlations among factors or among the levels of a factor. Assignments in the present sense ought to be distinguished from problems of assigning individuals to specified categories as is typical of the “assignment problem”.

This deterministic view can be extended to include random effects in each of the two modeling steps. Thus, the first step may be governed by a probability distribution of the assignments of objects to contribution vectors (sub-model 1), and at the second step each vector is provided with a probability distribution on potentially realizable trait states (sub-model 2). Herewith recall that each assignment corresponds to a mapping of the collection of objects into the totality of contribution vectors. One is thus concerned with a distribution of mappings. Combining both distributions one arrives at a probability distribution on all assignments of the members of a collection to trait states.

Since the actual objective is to use the potential outcomes of the model to explain the observations, the primary interest is in assignments that yield the actually observed trait states of the objects. More precisely, the subject of study is the totality of assignments of objects to contribution vectors that give rise to the observed trait states. This totality can be further narrowed by making assumptions on the initial conditions (which are occasionally referred to as “priors”) and by applying specific criteria to the qualification of each assignment to yield the observations. When probability distributions are considered, this amounts to studying the conditional probability distribution of the assignments given they allow for the observations. Even though it is not further elaborated in this paper, it should be noted that this probability distribution constitutes the stationary state distribution of the Markov chains applied in MCMC approximations.

The following examples will demonstrate the above-described model characteristics for a few established approaches to the analysis of latent factors.

3 Three examples

3.1 Linear model

A simple deterministic example can be obtained by letting $p_{\mathrm{1}},\mathrm{\dots },p_k$ denote the relative factor participations of k factors $F_{\mathrm{1}},\mathrm{\dots },F_k$ with real valued levels $f_{\mathrm{1}},\mathrm{\dots },f_k$ in the expression of a trait T. The factors F_i could be different types of nutrients available at different amounts f_i and interacting in different proportions p_i to produce a specific metabolic or physiological reaction T. A linear model of trait expression (sub-model 2) could be of the classical form

$$\begin{array}{}\text{(1)}& {\displaystyle }T(\mathit{p},\mathit{f})=\sum _{i=\mathrm{1}}^k{p}_i\cdot f_i\end{array}$$

familiar from factor analysis, where p and f denote the vectors with components p_i (factor loads) and f_i (factor levels), respectively, and the pair (p, f) of vectors defines a contribution vector. Unlike classical methods of factor analysis, the trait T here appears as a weighted average of the factor levels with no error term, where the weight vector p represents the factor participations. For any given vector f of factor levels, trait states of objects thus are real numbers in the interval specified by the smallest (min_if_i) and the largest (max_if_i) of the factor levels.

Turning to the specification of sub-model 1, objects could be assigned different relative factor participations p of factors, among which those are admissible that yield the observed trait states $t_j^{*}$, say, of the jth object. For the observed trait states to be realizable, the factor levels are required to satisfy the inequality ${min}_i{f}_i\le t_j^{*}\le {max}_i{f}_i$ for each object j. Given a fixed set of such factor levels, and assuming that there are no restrictions (or additional qualification criteria) on the factor participations p, there will always be at least one vector p(j) for each object j for which $T\left(\mathit{p}\right(j),\mathit{f})=t_j^{*}$. Hence, there may be many assignments of objects to contribution vectors (with a fixed set of factor levels) that yield the objects' observed trait states and are thus admissible. This may not hold true if sub-model 1 would require special conditions (constraints) to be obeyed by the (admissible) factor participations.

The fact that the observations can be explained by many assignments of objects to contribution vectors asks for further qualification criteria for the assignments that are desirable or even indispensable. A conceivably desirable criterion could be based on the perception that the contributions of factors act more beneficially the more balanced their participations are. Qualification would then increase with increasing evenness of the factor participations. Sufficiently low evenness could imply extents of imbalance that endanger the integrity of the system and would thus give rise to rejection of the model. The qualification criteria may then imply the decision to reject some of the components or even the whole model as an explanation of the observations.

Stochastic features can be introduced by declaring the factors $F_{\mathrm{1}},\mathrm{\dots },F_k$ and/or the relative factor participations $p_{\mathrm{1}},\mathrm{\dots },p_k$ as random variables with appropriate probability distributions. In this case the perhaps most common qualification criterion refers to the likelihoods of assignments that are admissible (i.e., that can realize the observed trait states under the restrictions of sub-model 1 and under the operation of sub-model 2). Qualification of factor contributions according to their balance as addressed above would then have to be integrated into the probability laws.

3.2 Metapopulation model A

A more complex situation arises if, for example, latent metapopulation structure is of interest, in which the constituent but unknown (sub)populations represent the (latent) factors. For genetic properties as traits of the objects (individuals), the most basic characteristics of the populations (i.e., their factor levels) will be sets of allele frequencies at any number of loci. In its first step (sub-model 1) the model then specifies the number of populations, the gene frequencies in each (sub)population, and the proportions of genes that individuals receive from the respective populations (contribution vectors). In its second step (sub-model 2) the model prescribes the mechanisms according to which the genes present in each contribution vector are combined into genotypes (e.g., via the mating system) and thus generate the genetic trait.

If the mechanisms rely on mating systems acting within one generation, for example, only two parents are involved in the formation of genetic types so that the contribution vectors cannot be composed of more than two positive components (with equal factor ∕ population proportions). Extension to several generations may then allow the participation of more populations representing the ancestors of individuals, which implies contribution vectors consisting of more than two components.

The probability laws involved in each step then allow computation of the probability for each observed genetic type of an individual to result from a given contribution vector (gene frequencies in populations and proportions of genes from populations) as well as the probability of the individual to be assigned to this contribution vector. Combination of both laws yields the conditional probability distribution of contribution assignments given the genetic types of the observed individuals. In particular, this results for each individual in a probability distribution of contribution vectors, from which one can compute, for example, the expected factor ∕ population proportions contributed to the individual's genetic type. In the same way it is possible to determine for each factor ∕ population the expected (relative) frequency of each allele across the contribution vectors of an individual.

More relevant information can be obtained by qualifying the contribution assignments according to their conditional probability distribution given the observed genetic types. The distribution quantifies the likelihoods of the individual assignments, which, in turn, represent one of the most common methods of qualification. The decision in favor of one or some of the assignments (meeting the qualification criterion) then rests on maximizing these likelihoods. Contribution vectors with their degrees of population mixture and allele frequencies within populations can then be directly determined. Considerations of this kind underlie one of the most popular population genetic model-based methods of revealing (sub)population structure (developed by Pritchard et al. (2000) and named structure¹). Many variants of Structure exist that address modifications of sub-model 1 (e.g., Falush et al., 2003, relating to correlations among allele frequencies; for a review of the variants of the method that concern sub-model 1 and sub-model 2 see Porras-Hurtado et al., 2013; also see Alexander et al., 2009).

3.3 Metapopulation model B

Another model of latent metapopulation structure proceeds from the idea that observed populations may in fact be connected by gene flow to extents that make some of them a single population. In this case, latent metapopulation structure results from merging observable populations in various ways into single hypothetical populations (Corander et al., 2003, with corresponding software Bayesian Analysis of Population Structure, BAPS). In addition to genetic type, this adds affiliation to observed population as a component of the observed trait. Each hypothetical population is now characterized by a genetic composition determined by the genetic types of the individuals present in the associated merged observed populations. The observed genetic composition in each hypothetical population is then considered to result from the operation of a hypothesized mechanism (sub-model 2) on an unknown prior genetic composition of the hypothetical population. The unknown genetic composition is usually again specified in terms of allele frequencies at a given number of gene loci, and the mechanism determines ways in which the alleles are combined into genotypes. Other ways of specifying prior genetic compositions are conceivable.

In this situation, hypothetical populations are the factors, their (prior) genetic compositions are the factor levels, and, since admixture of hypothetical populations is not considered, only one factor participates in each contribution. Moreover, assignment of an individual to a contribution vector is admissible only if the factor (hypothetical population) with positive contribution in the vector includes the individual's observed population affiliation. Since gene frequencies are defined for hypothetical populations, the gene frequencies in the contribution vectors to which individuals are assigned are the same for all individuals belonging to the same hypothetical population. This limits the set of admissible assignments of individuals to contribution vectors, and it is thus part of the modeling of assignments (sub-model 1) including specification of potential probability laws.

Depending on the number of observed populations, there may be many ways of partitioning the totality of populations into hypothetical populations by merging the observed populations. In each such partition the hypothetical populations establish factors of the kind explained above. Each partition can now be conceived of as a higher-order factor with levels defined by the hypothetical populations making up the partition. One thus arrives at a two-tier hierarchy of factors (as indicated above), in which the components of contribution vectors are each composed of a labeling of the partition and of a hypothetical population associated with the partition (the dimension of a contribution vector thus equals the number of hypothetical populations in a partition summed over all partitions). The levels of these multiple factors are again given by gene frequencies at a given number of gene loci. An assignment of the observed individuals to these contribution vectors is then admissible only if the partition label is the same in all of the assigned vectors. Qualification criteria must again be applicable to the thus defined contribution assignments.

Another approach termed Geneland by its authors (Guillot et al., 2005) is similar to BAPS but defines partitioning into hypothetical populations in a spatially explicit manner. In addition to their trait states, individuals are therefore characterized by their spatial locations. The partitioning is achieved by producing a Voronoi tessellation of the habitat area and merging the tiles of the tessellation into mutually exclusive sub-domains, the residents of which are considered to form hypothetical populations. Now the factors are spatially defined subpopulations, and the factor levels are again given by gene frequencies. As before, interaction among factors is not considered (only one factor participates in the contributions). Each partitioning of the tiles into subdomains defines a higher-order factor with levels provided by the subdomains in the partition. The set of partitions specifies the higher-order factors.

4 Qualification criteria for assignments and model validation

Many highly specific qualification criteria, attributes, and descriptors of these qualification criteria and attributes may be desirable. A trivial example is provided by the above linear model, in which assignments are disqualified if they do not provide nutrient types in sufficient proportions so as to realize the observed metabolic or physiological processes. Even if this were achieved, the stability of the processes could decisively depend on the kind of relations among the proportions with the result that more even proportions could guarantee higher stability and by this represent assignment of higher qualification. In metapopulation models A and B, similar principles of qualification could apply to the assignment of gene pools to genotypes if the genes present in a genotype either do not appear at all in the gene pool (disqualification) or appear at proportions that are more or less likely to give rise to the genotype under the hypothesized mating or migration system and mode of inheritance. The qualification criterion would in this case be governed by likelihood considerations.

After all, recalling that the analysis of cause–effect relations has priority in all deliberations (with contribution vectors as causes and trait states as effects) it is natural to consider ways of quantifying the strictness of these relationships as manifested in each assignment of individuals to contribution vectors. This is tantamount to measuring the degree of association of effects with potential causes and thus of the trait states of the individuals with their contribution vectors (realized in each assignment). As was shown by Gregorius (2011), association of a particular trait state with a particular contribution vector increases with increasing separation of this contribution vector from others not assigned to the particular trait state². Herewith, measurement of separation requires an appropriate measure of dissimilarity among contribution vectors (see Table 1). The individual associations can be summarized into a single measure of association of the trait states with the contribution vectors of an assignment. High degrees of association would then imply that individuals differing in trait state are more frequently assigned to distinct contribution vectors.

Table 1 Measuring dissimilarity among contribution vectors.

However, causal relations can also be viewed from the reverse (or dual) perspective in which trait states are considered to determine the factor contributions that can generate them. With environmental conditions as factors in adaptational processes, the two causal perspectives correspond to selection among phenotypic variants by the environment (e.g., via survival) and selection of environments by phenotypic variants (e.g., via migration). Under the reverse perspective, analyses thus refer to associations of factor contributions with trait states. Strong association would in this case be realized if individuals assigned to different contribution vectors differ more frequently and more distinctly in their trait states. The distinctness of the effect of a contribution vector therefore becomes apparent in the degree to which its corresponding group of trait expressions overlaps with groups corresponding to other expressions. Hence, distinctness of causes should show in distinctness of their corresponding groups of trait states. Quantification of this direction of association is meaningful only when based on a dissimilarity measure among trait states that indicates situations of complete distinctness by its maximum value.

As is suggested by the above explanations, the measures of association gain special relevance through their interpretation in terms of differentiation among trait states for their contribution vectors in the first case and differentiation among contribution vectors for their trait states in the second case (see Gregorius, 2011). Apparently, for complete differentiation in the first case, individuals assigned to the same contribution vector also share their trait state. This reflects the case of a proper cause–effect relation in that the same cause is not allowed to produce different effects. Moreover, distinctness of the causal variables involved in trait expression could be an important qualification criterion if only clearly distinguishable causes allow for reliable inference on the number of factors effectively involved in trait expression, for example.

In the second case, complete differentiation is realized if individuals assigned to different contribution vectors differ completely for their trait states. This does not exclude the possibility that individuals assigned to the same contribution vector may differ completely for their trait states. It thus allows for trait variation within groups but rules out trait similarity among members of different groups.

The degree of association can be treated as a qualification criterion akin to the likelihood by identification of assignments with maximum association. When probability laws are part of the model so that one obtains a probability distribution for the assignments, competing decisions as to qualification aspects may become relevant if maximization of likelihood and of association yield different assignments. Indeed, this is very likely to be the case since (as mentioned above) complete and thus maximum association of trait states with contribution vectors, for example, is obtained for assignments in which each contribution vector is assigned to only one trait state. Such assignments are almost always admissible. Therefore, it is appropriate to give priority to the likelihood qualification and evaluate the assignments of maximum likelihood for their associations.

Given the probabilities for the assignments to yield the observations, a presumably more consistent approach could however be based on the implied distribution of associations. In this context, a meaningful qualification criterion is suggested by the likelihoods (or posterior probabilities) of the associations. Maximization of these likelihoods yields assignments that allow for relevant inferences. Both perspectives, association of trait states with factor contributions, and vice versa are addressed here. For example, if among all feasible associations between trait states and contribution vectors (in either direction) the most likely ones should turn out to realize comparatively small association values, this would contradict the expectation that proper causal relations should range among the most likely. Such an observation would thus shed doubt on the appropriateness of the assumed probability laws or even the whole model structure. Both specification of assignments (sub-model 1) and trait generation (sub-model 2) could be concerned.

While this relates to a vital aspect of the analysis of latent causal factors, measures of association are but one type of descriptors of assignment characteristics. There are other assignment characteristics and descriptors that suit different purposes and could also serve as qualification criteria. For instance, in population genetic studies with supposed latent metapopulation structure as in the above three examples (relating to Structure, BAPS, and Geneland), genetic separation among latent (hypothetical) subpopulations is one of the most popular qualification attributes. This is especially relevant in metapopulation models B, in which each assignment is associated with a partitioning of the observed individuals into hypothetical subpopulations.

Since for these models the contribution vectors consist of only one factor contribution, separation among subpopulations can be determined for either the levels (hypothetical gene frequencies) of the factors (subpopulations) or the actually observed genetic frequencies in the subpopulations. To avoid ambiguity it should be presumed that in the assignments the same population should not be represented by different gene frequencies (assignment of individuals to the same factor implies identity of the factor levels). This is explicitly required in metapopulation model B but not in metapopulation model A, even in its version without admixture.

In the first case, in which separation among subpopulations is considered on the basis of hypothetical gene frequencies, cause–effect relations as introduced in the above association context are not at issue since the observed trait states are not explicitly involved. Nevertheless, measurements of separation among hypothetical subpopulations quantify the distinctness of populations as potential causal factors and could therefore be a relevant qualification criterion of assignments. Corander et al. (2003) recommend F_ST for “measuring genetic separation among populations”. Since F_ST is not a measure of differentiation or separation but rather of fixation or monomorphism of the populations (Jost, 2008), the recommendation is problematic as measured by its purpose. More appropriate alternatives are provided by indices of compositional differentiation (for an overview see Gregorius et al., 2014). Measures of partitioning of diversity (Jost, 2008; Gregorius, 2014) may not be appropriate either since they yield different values depending on the amount of diversity within the populations. Conversely, monomorphism of factor contributions could be a desirable qualification criterion for assignments when genetic drift in small and isolated populations is to be studied.

The second case of separation among subpopulations, which focuses on the observed trait states (genetic types) rather than on hypothetical gene frequencies, apparently received little or no attention in the relevant literature. This is surprising since the primary objects of analysis are the observed genetic types and the latent substructure among their carriers. In terms of associations, one is in this case concerned with association of subpopulation affiliation with trait state. In conventional experimental studies this direction of association essentially is the only one taken into consideration since it measures differentiation among communities.

The above considerations demonstrate that qualification criteria and their descriptors can be viewed to serve two purposes: (1) qualification of assignments and (2) qualification of the model. Assignment qualification can be classified as a problem of optimization theory in which objective functions are analyzed as to the “best available” values they can attain on a defined domain of inputs. Usually these values are maxima or minima of the objective function. In the present context posterior probabilities are examples of objective functions that have to be maximized on the domain of admissible assignments in order to obtain the desired assignment. Measures of association in turn can be used as means for assessment or validation of the model, possibly in combination with assignment qualification. In fact, maximum posterior probability can by itself also be used for model validation.

The constituent sub-models 1 and 2 of the combined model of latent factors contribute to its validation via restrictions made on the admissibility of the assignments (including assumptions on their prior distributions) and the mechanism that generates the observations from the contribution vectors. Problems of circular reasoning could emerge here if the specifications of sub-model 1 would anticipate the most qualified assignment (see, e.g., Mank and Avise, 2004). This would however require that the mechanisms of sub-model 2 are largely determined by the assignment specifications of sub-model 1, which, in turn, would lead to apparently tautological statements.

5 Assignment of observed objects to factors

Especially the metapopulation examples direct attention to the possibility of conceiving of latent factors as representing conditions that subdivide collections in concert with the modeled forces into separate groups of defined function. Reproductive, behavioral, or ecological compatibility or isolation of organisms may be considered factors, the functions of which give rise to the formation of groups. Joint ancestry or other separable forms of descent are further examples, not to forget the wide field of environmental stimuli. In some sense, such factors would define identities or origins of objects. However, in many of these cases, several factors contribute to an object's trait state, which makes it difficult to justify assignment of individual objects to just one factor. Exceptions are the above examples of latent metapopulation structure in which admixture of hypothetical populations is not taken into account (Structure with the option “without admixture”, BAPS, and Geneland).

A possibly more comprehensive approach to this problem is suggested by considering assignments of objects to single factors as a special case of a contribution assignment. Such assignments, which could be called “factor assignments”, are characterized by contribution vectors with one component of the relative factor participations equal to 1 and all others equal to 0. In a factor assignment all objects are assigned to such contribution vectors so that each object is associated with a single factor. Factor assignments are therefore special cases of contribution assignments. Since qualification criteria are defined for all admissible factor contributions, they apply in particular to the subset of (admissible) factor assignments, so that comparison of qualifications between general contribution assignments and factor assignments in particular is possible. In the population genetic context this relates to comparisons between models with and without admixture (migration, gene flow).

Maximum qualification can then be separately determined for factor assignments and for contribution assignments, for which the former cannot exceed the latter. However, the closer the maximum of factor assignments approaches the overall maximum of contribution assignments, the more support there is for the idea that the factors reflect “identities” or “origins” (including population or community affiliation) of the objects in the above sense. This would be all the more convincing if for each object in the contribution assignment of maximum qualification, the factor with the largest participation would equal the factor to which the object is assigned in the factor assignment of maximum qualification. Again, in the population genetic context this simply states that the population to which an individual is assigned in the absence of migration is also the population that contributes most of the genes present in that individual's genotype when migration is allowed.

The closeness of an assignment to a factor assignment can be quantified by considering the diversity of factor participations for each object. This is meaningful since the factor participations of an individual form a set of relative frequencies to which any acceptable measure of diversity is applicable. Preference might be given to explicit measures that vary between 1 and the number of participating factors with equality to 1 if only one factor participates and equal to the number of factors only if all of them participate equally. In this sense, diversity corresponds to the degree of admixture. The average of these diversities taken over all individuals thus establishes a reasonable assignment descriptor in that it becomes 1 only for true factor assignments and increases with the number of factors that effectively participate in an individual's trait expression.

6 Concluding remarks

Identifying assignments of maximum qualification as well as validation of the model are the primary goals in the model-based analysis of latent factors. It was pointed out that the former appears to be a special case of the general optimization problem, in which entities (such as assignments) from a defined domain are to be found that maximize or minimize an objective function. A large number of algorithms are available that may help to solve the optimization problem for complex situations by generating sequences of entities along which the objective function consistently increases or decreases, respectively (e.g., Boyd and Vandenberghe, 2009). Among these is the well-known expectation maximization (EM) algorithm that is designed for maximizing likelihoods and posterior probabilities. Yet, the EM method is rarely adopted, probably because of the limited range in which it was shown to operate efficiently (see, e.g., Alexander et al., 2009).

Apparently, MCMC algorithms belong to the most frequently employed methods in model-based analyses of latent factors, and this justifies briefly outlining their essential features and potential results. MCMC methods rest on Markov chains with states specified by the contribution assignments and stationary-state distribution given by the conditional probability distribution of the assignments that allow for the observations. Appropriate transition probabilities that guarantee convergence to the stationary distributions can always be obtained with Metropolis–Hastings or Gibbs algorithms, for example. The central result from Markov chain theory that is relevant for the analysis of assignment characteristics confirms that, when applying a real valued function to the states of a developing Markov chain, the average of the values converges with a probability of 1 to the expectation of this function realized for the stationary-state distribution (see, e.g., Roberts and Rosenthal, 2004). This implies that on the basis of efficient MCMC runs, one can estimate the expectation of real valued characteristics of the assignments including descriptors of qualification criteria of assignments.

It is essential to note that generally this does not include estimation of assignments of maximum likelihood or posterior probability. An exception is provided by small numbers of potential assignments so that their frequencies can be recorded by a finite number of indicator variables along an extending Markov chain. Yet, in most applications, such as the above examples of metapopulation models, potential assignments form highly dimensional continuous sets, which excludes their representations solely by indicator variables along Markov chains. However, suitable partitions of the descriptor range into intervals may at least allow for the identification of ranges of descriptor values of maximum probability. Explicit identification of individual assignments may not be possible. Nevertheless, when considering association descriptors, it is at least possible in this way to obtain an idea of the validity of the model by checking whether the most probable range comprises the largest associations (see above explanations).

Otherwise, one is confined to estimates of the expectation of real valued descriptors of assignments evaluated at the (stationary) assignment distribution. If all factors and their levels can be covered by descriptors (some in the form of indicator variables), joint convergence of their averages may help to identify an appropriate “expected” assignment. Provided the expected assignment belongs to the admissible ones, it need, of course, not be the most probable. This caveat applies especially to the above-detailed models A and B of metapopulations. The size of average associations in either direction can nevertheless be used in addition to validate the causal relevance of the model.

Moreover, a distinction has to be made between the expected association over the assignments and the association realized in the expected assignment. This might also be relevant for other assignment descriptors. As is mentioned above, consideration of expected assignments has substance only if they are admissible so that the respective descriptor is applicable. For example, if the model allows by definition only for single factors to be involved in trait expression (no admixture in the metapopulation models), factor assignment to individuals is specified by indicator variables (e.g., population affiliation of an individual). The average or expectation of an indicator variable, however, is not any more an indicator variable, so that descriptors that rely on such variables cannot be applied to expected assignments. This pertains for example to the BAPS model of Corander et al. (2003), who correctly consider the average (expectation) of the F_ST values of assignments to describe differentiation among populations (albeit addressing F_ST as a measure of differentiation is problematic as was recalled above).

In the same context it is worth mentioning that averages (or expectations) taken over population affiliations (as indicator variables) are difficult to distinguish from average (expected) degrees of admixture resulting from the corresponding models. It may therefore be appropriate to consider in the same model the above suggestion to treat factor assignments (absence of admixture; see Sect. 5) as a subset of all admissible assignments and compare the results obtainable from that subset with those from the total set of admissible assignments. The ambiguity inherent in expected population affiliations is avoided altogether when considering the expected individual diversity of factor participations as a descriptor of the degree of admixture. When comparing the measures of association with and without admixture (or factor interaction), information can be obtained about the strictness of cause–effect relations realized in the two situations. This can be realized either for expected associations or for distributions of association over appropriate partitions of the range of associations into intervals.