the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Models of poisoning effects on vulture populations show that small but frequent episodes have a larger effect than large but rare ones
Rigas Tsiakiris
John M. Halley
Kalliopi Stara
Nikos Monokrousos
Chryso Karyou
Nicolaos Kassinis
Minas Papadopoulos
Stavros M. Xirouchakis
Vultures are among the most threatened avian taxa in the world. When vultures aggregate in large numbers to feed, poisoned carcasses can extirpate entire populations at once. In the light of shrinking numbers worldwide, restocking and reintroduction projects, where wild or captive-bred vultures are released back into nature, constitute a crucial management tool, successfully implemented in many countries. However, reestablishment of sustainable vulture populations to their historical ranges remains a serious challenge, especially if the threat of poisoning persists, which is usually the case. In this study, we model the outcome of a restocking project where an initial colony is subject to repeated poisoning events. We use as an example the isolated population of the griffon vulture (Gyps fulvus) in Cyprus. Mathematical considerations and model simulations show that the probability of colony persistence depends on the initial population size and the intensity and frequency of the poisoning incidents. This type of scenario creates an Allee effect that requires a colony to exceed a minimum size in order to survive. Also in this scenario, a sequence of small but frequent poisoning episodes is worse on average than a few large and rare ones of the same cumulative mortality. Future population reinforcement efforts for vultures should focus on the release of adult birds in adequate numbers for the successful establishment of sustainable colonies and should involve a reduction in small but persistent sources of mortality such as the poison baiting of small canids that until now has been neglected by conservation scientists.
- Article
(476 KB) - Full-text XML
- BibTeX
- EndNote
Large scavenging birds of prey are a crucial component of the natural environment, providing one of the most important ecosystem services of avian taxa (Šekercioğlu, 2006; Moleón and Sánchez-Zapata, 2015). A relatively recent review has emphasized the significance of carrion as a huge reservoir of nutrients and energy and the crucial role of scavenging in food web theory and community ecology (DeVault et al., 2016). Obligate scavengers, like vultures, deliver a wide range of biological, ecological, economic and cultural services, but primarily they recycle dead biomass and affect the rate of energy flow within the ecosystem (DeVault et al., 2003; Moleón et al., 2014). In fact, scavenging is more critical in energy transfer than actual predation (Şekercioğlu et al., 2004); for example, a minimum of 124-fold more energy was transferred per scavenging link than was transferred per predation link of 10 food webs examined by Wilson and Wolkovich (2011). In the meantime, by consuming wildlife and livestock carcasses scavengers contribute significantly to the reduction in related health risks to humans from infectious diseases, which spread by population outbreaks of opportunistic scavengers hosting dangerous microbes (Pain et al., 2003; Markandya et al., 2008; Ogada et al., 2012). However, the ecosystem services delivered by healthy vulture populations have only recently been recognized following their large-scale decline or total collapse and the observed environmental and economic costs triggered by their absence (Prakash et al., 2003; Oaks et al., 2004; Markandya et al., 2008; Morales-Reyes et al., 2015; Panagiotopoulou et al., 2018).
At present, avian scavengers are among the most threatened species in the world (McClure et al., 2018; Safford et al., 2019). Their populations are endangered by various anthropogenic factors including food poisoning or contamination, reduction in available food supplies due to changes in livestock management practices and carcass disposal driven by new sanitary legislation, and collision with wind turbines or power lines (Šekercioğlu, 2006; Ogada et al., 2011; Margalida, 2012). Old-world vultures are long-lived species with low reproductive rates and delayed maturity; thus they have been particularly affected by anthropogenic mortality such as poisoning and persecution in the past (Whitfield et al., 2004; Hernández and Margalida, 2009). In Europe, all vulture species have continued to suffer severe population declines in recent decades due to the consumption of poison baits, which is still considered the most important threat to this avian group (Hernández and Margalida, 2009; Margalida, 2012; McClure et al., 2018; Margalida and Mateo, 2019).
The risk posed by baiting and the number of vultures affected depend on a number of factors, namely the type and amount of toxin used, the bait type and density (e.g., the number per unit area), and the time interval between bait placing and consumption. The most important factor appears to be the group size of foraging vultures that is related to the targeted poisoning animal, which could be a single small carnivore, a flock of large ungulates or even an elephant (Ogada et al., 2011; Parvanov et al., 2018). The infrequent large catastrophes are caused mainly after large-carnivore predation on big livestock (bovine, equine), when their kill remains are laced with agrochemicals, so the entire carcass can be considered a bait and subsequently cause the secondary death of numerous vultures (Stoynov et al., 2018). Poisoning, usually unintentional (sometimes also intentional), has proved to be the greatest threat to vulture populations globally, acting synergistically with other mortality factors such as collision with power lines or wind turbines (Ogada et al., 2015; Velevski et al., 2015; Vasilakis et al., 2016). Though poison baits are the most serious threat, international media attention has focused on impressive mass-poisoning events (Ogada et al., 2016; Henriquez et al., 2020), while more frequent events caused by baits aimed at small carnivores such as foxes and stray dogs are mostly ignored (Ntemiri et al., 2018). Recent field data using advanced technology (e.g., miniature GPS transmitters mounted on vultures) reveal that most of these poisoning events are not discovered (Stoynov et al., 2019). Though killing only a few individuals at a time, these baits may be the main constraint on the recovery of small and isolated vulture populations.
Current supplementary feeding schemes are developed following several different strategies (e.g., pure artificial, predator simulation, large “vulture restaurants”, small feeding sites near farms) and play a key role in vulture conservation especially in small and highly threatened population nuclei (Piper, 2006; Mateo-Tomás and Olea, 2010; Duriez et al., 2012; Moreno-Opo et al., 2015). However, vultures have an extremely complex foraging behavior involving social facilitation and information exchange mechanisms and perform long-distance movements, sometimes traveling hundreds of kilometers in search of food (Monsarrat et al., 2013; Kane et al., 2014; van Overveld et al., 2018, 2020; Peshev et al., 2021). This fact makes them especially vulnerable to a wide range of environmental hazards that are difficult to control, including poisoning (Ruxton and Houston, 2004; Houston, 2006).
Another approach is through reintroduction projects that attempt to reestablish sustainable populations within the historical range of each species by the release of wild or captive-bred individuals in cases where local populations are extinct (IUCN/SSC, 2013). Vulture reintroduction or restocking projects (the latter applies when local populations are not extinct but are not yet able to recover alone) have been applied with exceptionally positive results due to certain aspects of vulture biology, such as passive behavior, easy reproduction in captivity, and simple post-release food management through controlled feeding and easy adaptation in natural habitat through collective foraging with wild conspecifics (Houston, 2006). In the last few decades, reintroductions and restocking projects have been popular as a management tool for the restoration of vulture populations in Europe, Asia and America (Griffith et al., 1989; Wilson and Stanley Price, 1994; Bustamante, 1998; Terrasse et al., 2004; Sarrazin, 2007; Stoev et al., 2016; Stoynov et al., 2016; Colomer et al., 2020).
The aim of this study was to assess the risk of extinction of a typical vulture population due to poisoning. Emphasis was placed on limitations associated with small population size such as demographic stochasticity and other factors such as Allee effects that could affect the probability of species recovery (Deredec and Courchamp, 2007; Van Houtan et al., 2010). More specifically, we explored the effect of poisoning events in relation to their intensity (i.e., temporal frequency and mortality), focusing on the effect of large versus small poisoning events since the latter are most frequent in anthropogenic landscapes aimed at small carnivores.
In this context, the relevant research questions were as follows: (1) does one major poisoning event constitute a more serious threat than many small ones to the recovery of the species? (2) Do poisoning events accentuate the stochastic Allee effect of an already-small population? Our ultimate objective was to investigate the cumulative effect of demographic stochasticity and poisoning on the population dynamics and extinction probability of a species which has a wide range and is genetically close to most other old-world vulture species that numbered a million individuals until recently (e.g., the genus Gyps has 8 species from the 16 found in vulture guilds in Europe, Africa and Asia). For this we use two models: firstly, with a mathematical model we derive a simple measure of how the growth rate is affected by frequent poisoning events to test if frequent small events are more of a problem than large infrequent events of the same cumulative mortality. Then we use a second, more detailed, model of the population including demographic stochasticity, uncertainty in timing of poisoning events, age structure and density dependence to carry out a more realistic series of tests of the same question.
2.1 General background information on the study of population viability analysis
The present study used a simple mathematical (non-stochastic) population viability analysis (PVA) model. This model demonstrated the basic concept and gave a formula for the reduction in the growth rate and for the population size as a function of time in the presence of poison baits. Then we ran a more realistic PVA through simulations. We included demographic stochasticity and density dependence and also included randomness in the timing of poisoning events in the PVA, and we focus on the impact that overall poisoning incidences could have on the growth of the population. Population viability analysis uses modeling techniques to explore the population dynamics of rare or declining species and to estimate the probability of their persistence within a time frame and above a certain threshold of population size (Soulé, 1987; McGowan et al., 2011; Aresu et al., 2020). In our simulations we assumed relatively large ceiling populations (in the context of density dependence) to concentrate on the effect of the extinctions that happen when small numbers of introduced individuals fail to establish a breeding nucleus. In the present case, the results of a PVA could be used to predict the species population dynamics following a release and then to evaluate the impact of poisoning which could be reduced but not eliminated.
In order to parameterize our PVA, we used the available demographic, breeding biology and reproductive performance data for the griffon vulture (Gyps fulvus) populations in Cyprus and Crete (Charalambides and Neophytou, 1990; Xirouchakis, 2002; Iezekiel et al., 2004; Xirouchakis, 2010). The Cyprus colony exemplifies the kind of situation faced by many vulture populations, being isolated and suffering frequent losses due to poisoned baits. This population was also the subject of a restocking project between 2011 and 2015 (Kassinis et al., 2015). The Cyprus population is the subject of one of three recent griffon vulture restocking projects in the Mediterranean islands along with populations on Sardinia and Sicily (Mereu et al., 2017; Aresu et al., 2020). In all these projects, population recovery has been jeopardized by poisoning events, mostly due to poison baits aimed at foxes, canids, etc. (Grussu and SAG, 2019). In Cyprus reductions in food availability due to land use changes (e.g., urbanization due to touristic development, legislative constraints on carrion disposal) have put the species under further pressure (Iezekiel et al., 2004). During the 1960s, the population on Cyprus consisted of at least 100, but by 2012 it numbered only 11–12 individuals (Kassinis et al., 2019). This alarming fact led to initiation of an urgent restocking project. A total of 25 wild-born, rehabilitated individuals originating from Crete were transported to Cyprus during 2011–2014 (Stavrinides, 2019), though 2 died before their release and 3 were unable to adapt because of imprinting. Auxiliary conservation actions included acclimatization of the birds in proper aviaries, construction of several supplemental feeding sites, and public awareness campaigns in the national media and in local schools. All these birds together with two fledglings born in Limassol Zoo were released successfully in the wild and were monitored by radio tracking and by camera traps positioned close to the artificial feeding sites. However, a poisoning incident in the winter and spring of 2015/16 killed at least 11 griffon vultures (Stavrinides, 2019). Currently (2020–2021) only one small population nucleus remains on the island hosting approximately 20 individuals. This includes at most three egg-laying pairs, and most of these are from restocked individuals (Kassinis et al., 2019). This amounts to a net loss of population since the restocking program.
Poisoning of vultures in Cyprus is a characteristic example of the worldwide phenomenon of the “small type” of poisoning attributed to the use of baits against small canines that has never before been assessed in depth. In particular, the only top predators of the island, namely red foxes, feral dogs and cats, prey on small game species and newborn livestock. On Cyprus, there are no events on the scale of the mass poisonings of vultures such as those by elephant poachers in Africa, those provoked by wolf kills in the Balkans, or those where entire carcasses of large ungulates are laced with toxic agrochemicals (Xirouchakis et al., 2000; Ntemiri et al., 2018). Instead, we observe relatively small-scale ones such as individually poisoned canids that are consumed by a handful of vultures (Iezekiel et al., 2004; Ogada et al., 2012; Ogada, 2014). The model used in this paper can be applied to other areas worldwide (with the appropriate choice of parameters), but more importantly it is especially focused on reintroduction and restocking projects where initial populations are extremely small.
2.2 Basic mathematical model
We assume a simple model with an initially small, density-independent vulture colony of size N0 (i.e., autochthonous plus restocked birds) subject to births and deaths. This may be described in discrete time by a simple linear growth model (ignoring stochasticity and age structure; see Appendix A) with a yearly growth rate r given by the birth rate minus the death rate. When these rates do not vary in time and the birth rate is higher, the population is expected to grow exponentially or, if the death rate is higher, to decline exponentially. However, in real populations that are small, this pattern is strongly affected by demographic stochasticity, which can lead to decline or extinction even when the populations are expected to grow. In a newly formed griffon colony, variations in the birth rate can happen for a variety of reasons such as the failure of adults to mate, the improper social structure of the breeding group or other individually based effects (Grimm and Railsback, 2005; Lomnicki, 2011).
We assume that conditions, in the absence of poisoning, are good, so that the instantaneous rate of change in population size per individual (linear growth rate), r, is positive. Poisoning can be described by adding an extra mortality of specified frequency and value (i.e., the number of dead vultures per poisoning incidence). Assuming that a poisoning incidence occurs on average every T years and kills each time exactly D individuals at random in the population, it is possible to show (Appendix A, Eq. S4) that the growth rate modified by the presence of poison baits is
Here N is the population size. Equation (1) shows that the reduction in the growth rate is less severe for larger population size. It is also evident from Eq. (1) that there is a critical population size and if population exceeds this, then the resulting growth rate is positive but if it is smaller than this critical size then the growth rate is negative. If the growth rate r′ becomes zero, then it is evident that the population is at the minimum viable population size. This critical value, M, considering that this very small initial population has not reached the carrying capacity, is given (Appendix A, Eq. A5) as
The value M can be understood as a conditional minimum viable population (MVP; Fagan et al., 2001; Flather et al., 2011) that arises from the poisoning imposed on the population. Equation (1) shows that the reduction in the growth rate is more serious for small populations and as such constitutes an Allee effect. It is also evident that if a big poisoning event occurs, then the whole population could be extirpated. The structure of this MVP reveals that the gain through regular population growth between episodes should be greater, on average, than the number of individuals lost in an episode. Thus, for a population N to be viable we require N>M. If there is a large mortality episode of magnitude D every T years, then by the time of the next episode at t=T, the population will have reached a size of N0Exp(rT) and will fall by D again after the next poisoning event. Immediately after the nth poisoning event, the population will be
This equation has a different limit in two different situations. As shown in Appendix A, firstly, as baits become bigger but less frequent we have
On the other hand, when the baits are big but rare, with rT≫1, we have
Here, m is the number of deaths per unit time due to poison (see Eq. A8 in Appendix A). Thus, making baits smaller and more frequent always depresses population, while making baits larger but less frequent in the limit becomes less important in its effect. This demonstrates that theoretically many small events could be worse than a few large events of the same total mortality compared to what the simulation population models predicted. Note that the relations (Eq. 4) reflect average behavior. A single badly timed large event could wipe out a whole population at once before it has time to recover, thus impacting a population more seriously than a series of small events.
Table 1Parameter values used in simulations in this study, including those that change according to the different model runs. Demographic parameters (e.g., reproductive success and survival rates based on data from the griffon vulture population on the island of Crete, after Xirouchakis, 2002, 2010). The parameter T is the expected time for the exponentially distributed waiting time for which the 95 % interval will be (0.0253T, 3.69T).
2.3 Simulation model
To make a more realistic forecast of the population dynamics in the presence of catastrophes, a simulation model was used. A large range of simulation models are available for a wide spectrum of needs (e.g., see Grimm and Railsback, 2005). The simulation model used in this study, written in C, was based on an earlier study (Hoelzel et al., 1993; Halley and Hoelzel, 1996). Although the earlier studies made extensive use of the capacities of this program to follow the genetics of a population, genetic consequences lie beyond the intended scope of this study. The program works in a similar fashion to packages such as Vortex (Lacy and Pollak, 2014) which have also been used in vulture PVA studies (Aresu et al., 2020); see flow chart (Appendix B). Our program uses a demographic structure like a Leslie matrix model but with discrete individuals. The program runs the model a specified number of times to obtain this number of replicates for every set of parameters. Each run of the model traces the fate of all individuals in a small colony. Individuals are independent but subject to the same demographic parameters. At every time step, each individual is subject to mortality and the opportunity to reproduce. This mortality depends on the age and sex of each individual, which dies or progresses to the next age class according to a Bernoulli trial for each year whose probability is based on the age-specific survival coefficient. Females mate and give birth to offspring with a Poisson random variable with a parameter equal to the annual fecundity for that age class. Originally this application was developed for the study of the effects of different types of population catastrophe on small colonies and is thus ideal for this study. Catastrophes are modeled by events that happen at random according to a specified frequency of occurrence. If such an event occurs, its impact is fixed and exactly this number of individuals is removed from the population, their identities being chosen at random irrespective of sex or age.
The demographic parameters for the population of griffon vultures in Crete were adopted and used for yearly survival and fecundity, and these provided the demographic constants such as age-specific mortality and fecundity (Table 1). The first-year survival rate (s0) ranges between 0.3–0.5 (Xirouchakis, 2002, 2010), but we set s0 close to the lower limit, namely 0.35, since larger figures produced unrealistic values of the growth rate. We assumed older individuals had survival rates of 0.75, 0.8 and 0.9 for the second, third and fourth year, respectively, and 0.95 thereafter. We assumed that each female beginning in its fifth year could produce and raise one offspring per year. Improved procedures of parameterization in the event of parameter uncertainties could be applied, such as shown by McGowan et al. (2011), but these are beyond the intended scope of this study. Density dependence is imposed by means of a ceiling condition: if the population finds itself close to this ceiling, only as many new individuals are recruited to the population as there is room for. The program ran the model 1000 times for 1000 years of model time for every set of parameters. In the absence of poisoning events, our assumptions lead to exponential growth, with a growth rate of r = 0.07 for the parameters used. In simulations, we assumed that a poisoning event of fixed magnitude (D) happened on average every T years. This was performed by allowing events to happen each year with a probability of , thus ensuring an average rate of and hence an average time between events of T. Poisoning often takes place when someone puts a poison bait in the field or by poisoning the carcass of an animal; thus the number of vultures affected corresponds to the bait or the carcass size. Recent information from the field suggests that such poisoning events of vultures occur in Cyprus approximately once a decade (Game and Fauna Service, unpublished data), which would suggest a value T≈10. If the “delivery mechanism” is a dead animal contaminated with poison, then this could kill several vultures. In our simulation model we explore events of different fixed impact (i.e., different D). In this model, density dependence was included through an upper limit on the total population. We ran this model for a set of scenarios involving different sets of the parameters. These included values for D of 1, 10 and 30 individuals and for T of 1, 10 and 30 years. We considered a different initial population size N0 of between 5 and 100.
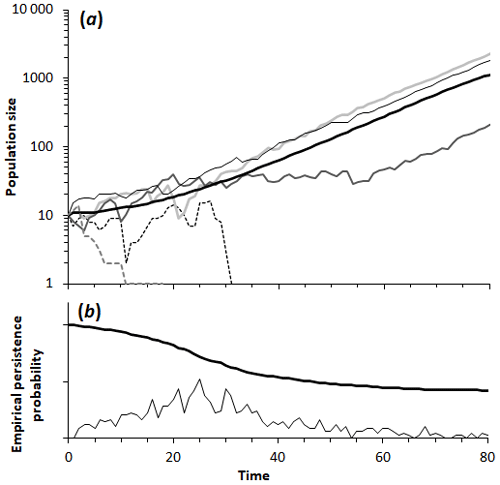
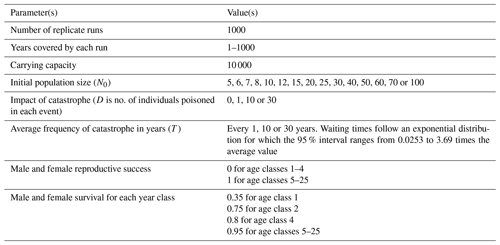
Figure 1(a) Sample of five population trajectories as a function of time generated by the simulation model (using the same parameters), showing two extinctions and three iterations in which the population persisted. The thick black line is the average of 1000 simulations. (b) Empirical persistence probability, based on the surviving populations (thick black line) and the number of new extinctions out of the 1000 simulated populations, both as a function of time. By t=50 most populations have either gone extinct or reached a population sufficiently high that extinction is improbable. Parameters: initial population is 10; impact of catastrophe is 10 deaths; average time interval between catastrophes is 10 years (95 % interval is 0.253 to 36.9 years); carrying capacity is 10 000.
Our simple mathematical model of population shows the effect of frequent poisoning events on population dynamics and yields quantitative estimates of the population growth rate. When a population with a positive growth rate (r>0) is subjected to poisoning events, the effect is to depress the growth rate. In the presence of poison baits, the growth rate decreases when the population size decreases, as it does with an Allee effect. For a sufficiently small population, the growth rate may become zero; this is the minimum viable population (MVP; Fagan et al., 2001; Flather et al., 2011). Thus, for viability a population N must exceed this value (N>M). If the population exceeds this, the resulting growth rate is positive, but if the population is smaller than this critical size, then the growth rate is negative. The structure of Eq. (2) reveals that the gain of individuals through regular population growth between episodes needs to be greater, on average, than the number of individuals lost in an episode (N>M). Equation (3) also shows (see Appendix A) that a sequence of small, frequent poison baits can be worse for a colony than a sequence of large catastrophes with the same total mortality, as small, frequent events have greater impact on growth than large but very rare ones that have a negligible effect on an otherwise healthy population. Of course, if such an event does happen in the initial stage, it can extirpate the whole population in one poisoning episode. The more realistic simulation model, where the timing of poisonings is random with an average frequency , supports these findings. Simulation runs with the same parameter set show that a population may survive or become extinct when the population is small (Fig. 1).
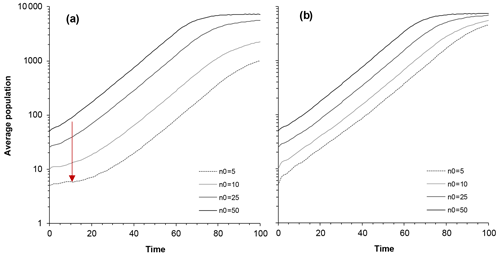
Figure 2Model predictions for average population size as a function of time and different restocking (initial) population sizes: N0 = 5, N0=10, N0=25, and N0=50. (a) Population size average over all populations, including extinct ones. The depression in the initial phase (red arrow) reflects the Allee effect. (b) Average population size only for populations that eventually survive. Impact of catastrophe is 30 deaths; average time interval between catastrophes is 30 years (95 % interval is 0.76 to 111 years); carrying capacity is 10 000. (The vertical scale is logarithmic, so regular, density-independent growth should follow a straight line.)
In the early stages of a newly formed colony, when the population numbers tens of individuals, the extinction probability remains high, but once the population becomes large, the extinction probability becomes negligible. Furthermore, the growth of the population suggests that an Allee effect is present depending on the initial group size (Fig. 2). A delay in the population growth rate is thus prominent among populations where the initial colony size is small (Fig. 2a). In contrast, this pattern is rather muted when we consider only the populations that survived (Fig. 2b). The discernable leveling off of population growth above 1000 individuals is density dependent because the population has a ceiling at 10 000 (Fig. 2). The leveling off (Fig. 2a) below 10 000, associated with smaller initial populations, is because there are more extinct populations leading to a lower average. Given the same amount of deaths per unit time, the impact of small and frequent poisoning incidents was more significant than the impact of large but rare ones.
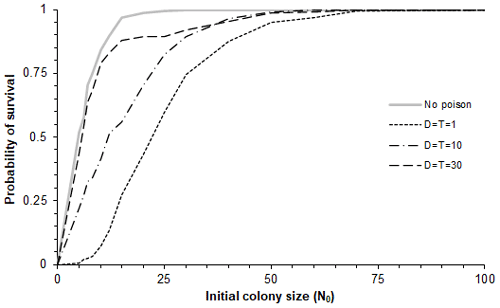
Figure 3Model predictions for the probability of survival as a function of different restocking (initial) population sizes and different impacts of catastrophes. In each case involving poisoning, the cumulative loss rate due to poison is one individual per year. Thus, for the three curves for which the numbers of individuals poisoned in each catastrophe (D) were 1, 10 and 30, the corresponding frequencies of poisoning events (T) were once every 1, 10 and 30 years, respectively, with 95 % intervals (0.0253T, 3.69T) in each case. The initial population sizes used were 0, 5, 6, 7, 8, 10, 12, 15, 20, 25, 30, 40, 50, 60, 70 and 100.
More specifically by investigating the probability of population survival as a function of initial colony size (N0) for four scenarios with different poisoning intensity, namely (a) small and frequent (D=1), (b) large and rare (D=30), (c) intermediate (D=10), and (d) no poisoning, showed that for any starting colony size, the survival rate is lowest for small, frequent events (Fig. 3).
We also found through simulations that for models with different ceiling values (100, 200 and 10 000), the results were rather insensitive to the value of the ceiling (Fig. 3). The proportion of populations surviving in the three cases is more or less the same, with the coefficient of variation between them being less than 5 %. Thus, the basic persistence probability will not be so sensitive to changes in the ceiling value (or carrying capacity) if this is greater than 100 individuals.
Poisoning events range from small but frequent to large but rare. Media headlines tend to concentrate on large-scale catastrophic events with the power to shock (Smith, 2021; Murn and Botha, 2018), neglecting the importance of small ones. In this study, the values of the respective model simulations were chosen with a constant ratio , meaning that the number of poisoned vultures per unit time remained the same on average. We have shown that a sequence of small, frequent episodes of poisoning is expected (on average) to have a higher impact on the population than a few large, infrequent ones for the same cumulative mortality (Fig. 3). This can be understood by the fact that a growing population recovers exponentially in long time intervals and this geometric growth advantage is lost if intervals are small.
Poisoning events of this kind also induce Allee effects which are associated with minimum viable population sizes. Therefore, in a conservation context this can make it much more difficult for a colony to become established if it is initially small. Similarly, the initial population size has also been found to be critical, through applying different PVA models, for the two remaining griffon vulture colonies in Sardinia (Aresu et al., 2020). Specifically, there is no point in establishing a colony that is smaller than the MVP: (where r is the population growth rate of the vultures and where poisoning occurs on average every T years killing each time D individuals). The minimum viable population represents an important threshold, but, in the presence of environmental and demographic uncertainty, there is no certain outcome. In this context the extinction of the founder colony does not necessarily imply poor management, since even populations with N0<MVP might still survive or those with N0>MVP might still go extinct. In the present case this type of Allee effect is manifested in small initial populations that grow more slowly than larger ones when they are close to the critical number of vultures needed to be released for the recovery and the safeguarding of the species in the long term. This underlines the great need for the creation of large-sized sustainable vulture colonies. This in turn demands a large reservoir of birds available for restocking. The Allee mechanism emerging from this model, based on poison baits, is distinct from Allee effects associated with communal foraging (where large colonies share effort and hence improve survival rates, especially if food is scarce and widely scattered) or with genetic effects (Berec et al., 2007). If either of these other effects were to be present, the result would be to increase the strength of the Allee effect and raise the size of the MVP. Our model is based on demographic parameters without explicitly considering food as a limiting factor in contrast to other studies where there is more explicit treatment of food energetic requirements (Colomer et al., 2011; Margalida et al., 2018).
These results were supported using a combination of arguments from mathematical models and from simulations. The purpose of this paper was primarily to demonstrate the possibility of these things happening. In this case our approach of parameterizing the simulation model on the basis of average values based on the population in Crete is appropriate. Should specific, targeted management be required for the single population in Cyprus, a more systematic approach to parameter uncertainty might be considered (McGowan et al., 2011).
So, consistent with intuition and experience, a substantial initial group size is needed to offset mortalities due to poison baiting, consistent with the predictions of many demographic and genetic studies demonstrating that the persistence time of a colony increases with initial size (Shaffer, 1987; Griffith et al., 1989; Allen et al., 1992). Specifically, if poisoning events of impact D (i.e., the number of dead vultures) happen every T years and the species has a yearly growth rate r, the colony size should always be well in excess of birds in order to have a sustainable population. In this context, the restocking success would strongly increase by using already-paired breeding adults among the released founders, as this would lead to a larger effective population size which is generally a small fraction of the total population (Frankham, 1995; Sarrazin and Legrende, 2000). Our results were obtained using a model developed specifically for the parameters of the population of griffon vultures in Cyprus but are expected to be relevant to most vulture species in any place worldwide whenever restocking is used as a conservation tool.
In the absence of a stable breeding nucleus of griffon vultures on Cyprus (i.e., four to six individuals) and with the lack of other nearby mainland colonies, the restocking scheme could be seen as a colonization process. In this case, its success would be largely determined by habitat suitability, the species ranging behavior and its reproductive performance (Le Gouar et al., 2008; Knowlton and Graham, 2010). Given that the foraging and breeding habitat remains intact and within the dispersal abilities of griffon vultures, the promotion of breeding activity might be a good short-term conservation target, which would lead to a higher growth rate (see Eq. 1) and lower MVP (Eq. 2). This could be achieved by taking advantage of the species' high gregariousness and conspecific attraction (Mihoub et al., 2011), which has shown to be the main driver for the creation of new colonies (Sarrazin et al., 1996; Le Gouar et al., 2008). By supplementary feeding close to old traditional breeding or roosting cliffs, these sites would facilitate potential breeders to locate mates as well as providing safe, non-contaminated food (Bijleveld et al., 2010; Mateo-Tomás and Olea, 2010). Consequently, effort has to be focused on certain areas and time periods, as poison bait occurrence does not happen at random as in our simulations but exhibits a characteristic spatial pattern (i.e., in pastoral and hunting areas) and a distinctive period of manifestation (i.e., in the lambing or pre-shooting season).
Therefore, as small canids (e.g., feral dogs, foxes) continue to be poisoned very frequently globally but are frequently overlooked due to species-dependent detection bias that underrepresents such animals (Gil-Sánchez et al., 2021), we expect that small numbers of dead, poisoned vultures will similarly be unnoticed especially in remote places, while only major poisoning events are expected to be found easily and registered officially. This unintentional (secondary) poisoning (Xirouchakis et al., 2000), although difficult to reveal in situ, may be one of the biggest threats to vultures worldwide (Botha et al., 2017) and could explain why small, isolated vulture populations where they still exist continue to decline or are unable to recover. Clearly, small poison events should be targeted by authorities to attract the attention they deserve, as they could eliminate other endangered raptors too and be a critical determining factor in the species' population dynamics especially if they affect adult age classes of species with low reproductive rates (Hernández and Margalida, 2008).
The colony of Gyps fulvus on Cyprus still remains critically endangered. Fresh action started in 2019 via a new restocking project aiming to transfer and release at least 24 individuals of Spanish origin into Cyprus over a 2-year period. The conservation actions needed for the survival of such a small group are primarily to do with protecting the colony from poisoning such as by constant supplementary feeding and an extensive anti-poisoning campaign, e.g., by using specially trained anti-poison dogs (Ntemiri et al., 2018). There should also be some constantly monitored individual vultures tagged with GPS-tracking devices, a cheap method for locating small poisoning events over extensive rough areas (Stoynov et al., 2019). This will allow the creation of (poison-free) “vulture safe zones” (VSZs; see also IUCN Bangladesh, 2016; Botha et al., 2017). Locally adapted VSZs are critical for maintaining the population nucleus relatively safely. Since the use of poison baits to kill predators is based on complex socio-economic factors in rural areas, anti-poisoning action plans should be applied worldwide according to the specific peculiarities of each area (Safford et al., 2019). Alongside this, it is important to boost populations via targeted restocking projects. Such actions may also need to overcome Allee effects by ensuring minimum viable populations.
In conclusion, while the public concern over shrinking vulture populations has focused mainly on large mass-poisoning events, we have shown, through mathematical models and simulation, that a sequence of small episodes may actually be worse than a few large but rare events that cause the same overall mortality. Future population reinforcement actions for vultures will most likely be successful if many adult individuals are released simultaneously in poison-free vulture safe zones around remaining colonies so as to maximize initial density and minimize Allee effects. In the meantime, such action could promote social facilitation and the formation of new griffon vulture colonies throughout their former ranges, which could also be important for the other seven Gyps species, as well as for other vulture species worldwide that are threatened with extinction.
In this appendix we describe the mathematical aspects of the model in greater detail. We assume that the population of vultures consists of a small colony subject to births (b) and deaths (d) but not density dependence. This may be described in discrete time by the following simple equation:
Here d is the annual mortality of individuals, ignoring age structure. The growth in this system is exponential growth (if b>d) or decline (if b<d) provided b and d are constants which do not vary in time. However, in reality when populations are small, b and d are strongly subject to demographic stochasticity, which can lead to declines or even extinction even when b>d. In a new colony, variations in the birth rate, b, can happen for a variety of reasons such as the failure of adults to mate. Random variations include individually based effects. Other issues that may affect small populations are Allee effects caused by genetic, behavioral or anthropogenic factors. We do not consider such factors in this study apart from the effects of poison baits. In reality, poisoning events happen at random with a random size. Nevertheless, we can usually assign a characteristic frequency and a characteristic size. In the simulation model in the text we explore this with simulations. Here, we use a simple mathematical model to show that (a) there is an Allee effect and an associated MVP and (b) many small events are worse than a single large one.
Estimating the effect of poisoning on the population growth rate
Poisoning can be described by adding an extra mortality of specified frequency and value (i.e., the number of dead vultures per poisoning incidence). Assuming that a poisoning incidence occurs on average every T years and kills each time exactly D individuals and R is the replacement rate (the growth rate r is actually the natural logarithm of R), the species population dynamics is described by the following equation:
The replacement rate for T years is
We assume that the replacement rate is greater than unity for the population to grow. Thus from Eq. (A2), it becomes evident that if the starting population size does not exceed a certain value of at least
which is essential for colony survival, it will not grow. This threshold is the associated minimum viable population (MVP).
Evaluating the Allee effect on the population growth rate
The growth rate is the logarithm of the replacement rate. If the intrinsic growth rate, r, is small but positive, then the modified growth rate can be found from Eq. (A3) as follows:
For this approximation (a Taylor series expansion of the logarithm) to hold, we require that the terms in are small relative to 1. Overall, the growth rate would be reduced for small populations, equivalent to an Allee effect. The modified growth rate becomes zero at a population of . For a population N0 to be viable we require N0>M. Thus, the associated minimum viable population (MVP) is
which is also Eq. (2) in the main text. This reflects that the gain through regular population growth between episodes should be greater, on average, than the number of individuals lost in an episode.
Impact of small and frequent versus large and rare catastrophic events
We can rewrite Eq. (A2) in terms of the growth rate:
If we define ρ=exp(rT), then we can say that
We can also rewrite this (starting with t=0 so that N(t)=N0) as
which is Eq. (3) in the main text. We can also define t0=nT so that we have
Note that the first term is independent of the size, D, and frequency, T, and so is the second factor of the second term, so everything comes down to the factor . Now suppose the number of poison baits per unit of time is constant so that
Then we can rewrite the above as
Clearly, the amount of poison per unit time, m, decreases that population at time t0, N(t0). However, the distribution of poisoning is also significant. The population N(t0) increases as T increases because the factor depending on T, in square brackets, decreases with T. More specifically, if T is small so that rT≪1, then so that
The limit is
In the other limit, when rT≫1 we have
Based on this limit, the effect of making baits smaller and more frequent always depresses population, while making baits larger but less frequent in the limit becomes negligible in its effect. This demonstrates that many small events are worse than a few large events of the same total mortality, comparable to what the simulation population models predicted.
In this appendix we describe the simulation model using the ODD protocol of Grimm et al. (2006). The basic idea of the protocol is to structure the information about an individually based model as a sequence of seven elements in three blocks: ODD means overview (purpose, state variables, scales), design concepts and details (initialization, input, submodels). We will refer to our model within this framework. Our simulation model was specifically designed to incorporate population genetics. However, since that aspect is not used in this paper, we will not refer to it.
B1 Purpose
The purpose of this program is to see how age-structured populations respond to various highly structured environmental mortality events, such as bottlenecks and repeated poisoning events, especially when these populations are small.
B2 State variables and scales
The state variables consists of sub-populations of discrete individuals. Populations are characterized by the state variables of age and sex. There is only a single population, and there is no spatial component. The shortest timescale is a single year. The longest timescale can be chosen to any length, but common choices are typically less than 1000 years. There is a fixed maximum lifetime for each animal, T, which determines how many age classes there are.
B3 Process overview and scheduling
The model proceeds in annual time steps. Within each year or time step, several stages happen. These are imposed mortality (e.g., by poisoning), natural mortality and reproduction.
B4 Design concepts
Emergence. Population dynamics emerge from the basic demographic parameters and from the stochastic processes underlying morality and reproduction.
Interaction. There are two types of interactions: reproduction can occur for any female if there is at least one male present in the population at the time. Density dependence occurs through a ceiling mechanism. If there are more new individuals born than allowed by the carrying capacity, then there is no reproduction that year.
Stochasticity. All demographic parameters are interpreted as probabilities or are drawn from probability distributions. Imposed mortality is defined by the number of killed individuals (D)T and is carried out by selecting D individuals from the entire population at random. Natural mortality is defined by the probability of each individual in each age–sex class of surviving. Thus, if there are N animals in an age class and their survival probability is s, then the number surviving is a binomial random variable of N trials and probability s. The number of births from each age class is the number of females of that age weighted by the probability of reproductive success or the number of offspring. Each offspring is male or female with a probability of 50 %.
B5 Initialization
The evaluation of each simulation run started in the first year when the number of model animals was equal to N0 individuals. These are chosen to be male or female with 50 % probability. The numbers in each age class are chosen from a multinomial distribution at random. The maximum lifetime, T, determines the number of categories, and each category k is associated with probability of success pk, which is proportional to the probability of survival to age k.
B6 Input
Imposed environmental conditions are classed as “input” and often change either randomly or according to a set pattern. In our model the only such input is the externally imposed mortality (i.e., poisoning), which is fixed by the user (see Table 1).
B7 Submodels
The initial population is chosen by sampling at random N0 individuals from the age-dependent probability mass distribution where pk is defined as follows:
Here s0, s1, …, sT−1 represents the survival probabilities associated with each age class.
B8 Flow chart
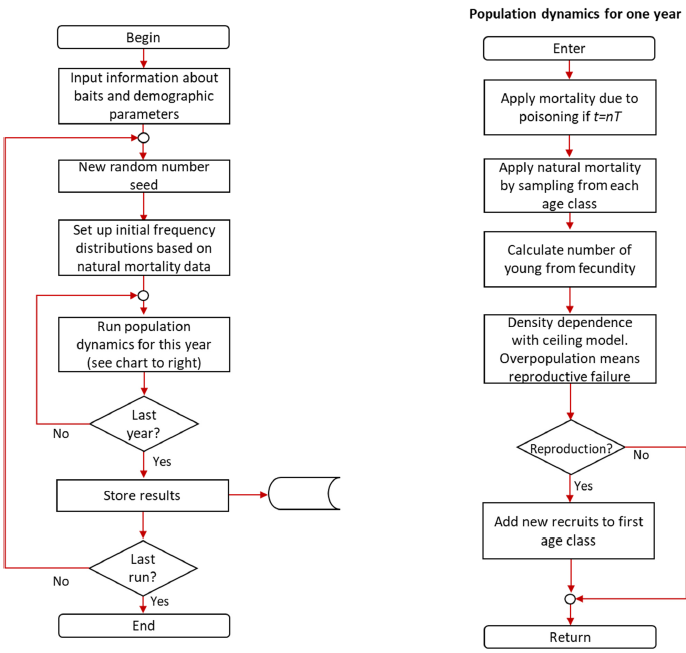
Code may be found in the Open Science Framework repository (https://osf.io/tnvuh/?view_only=205bcf1f4a274c579591454827023b79; Halley, 2019).
No external data sets were used. The only data used are in Table 1, which are from published sources.
RT coordinated the writing, collected all written material, wrote a substantial part of the paper and made the synthesis; JMH conceived the theoretical idea and designed and supervised the mathematical modeling procedures; KS substantially edited the paper; NM supervised the research and helped the modeling procedures; CK ran the modeling procedures; NK and MP coordinated the fieldwork and collected all field data; SMX initiated the project, provided all field data, formulated the hypothesis to be tested and wrote a substantial part of the paper.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the editor and two anonymous referees for helpful suggestions on the manuscript.
This study was funded by the European Regional Development Fund and national funds of Greece and Cyprus through the Cross-Border Cooperation Program Greece–Cyprus 2007–2013 project “GYPAS: Strengthening the Cypriot population of Griffon Vultures (Gyps fulvus) with individuals from Crete (Greece)”.
This paper was edited by Kurt Jax and reviewed by two anonymous referees.
Allen, E. J., Harris, J. M., and Allen, L. J. S.: Persistence-time models for use in viability analyses of vanishing species, J. Theor. Biol., 155, 33–53, https://doi.org/10.1016/S0022-5193(05)80547-8, 1992.
Aresu, M., Rotta, A., Fozzi, A., Campus, A., Muzzedous, M., Seccis, D., Fozzi, I., Rosa, D. D., and Berlinguer, F.: Assessing the effects of different management scenarios on the conservation of small island vulture populations, Bird Conserv. Int., 31, 111–128, https://doi.org/10.1017/S0959270920000040, 2020.
Berec, L., Angulo, E., and Courchamp, F.: Multiple Allee effects and population management, Trends Ecol. Evol., 22, 185–191, https://doi.org/10.1016/j.tree.2006.12.002, 2007.
Bijleveld, A. I., Egas, M., Van Gils, J. A., and Piersma, T.: Beyond the information centre hypothesis: communal roosting for information on food, predators, travel companions and mates?, Oikos, 119, 277–285, https://doi.org/10.1111/j.1600-0706.2009.17892.x, 2010.
Botha, A. J., Andevski, J., Bowden, C. G. R., Gudka, M., Safford, R. J., Tavares, J., and Williams, N. P.: Multi-species Action Plan to Conserve African-Eurasian Vultures. CMS Raptors MOU Technical Publication No. 5, CMS Technical Series No. 35, Coordinating Unit of the CMS Raptors MOU, Abu Dhabi, United Arab Emirates, 2017.
Bustamante, J.: Use of simulation models to plan species reintroductions: the case of the bearded vulture in southern Spain, Anim. Conserv., 1, 229–238, https://doi.org/10.1111/j.1469-1795.1998.tb00033.x, 1998.
Charalambides, C. M. and Neophytou, P.: Birds of Cyprus, Nineteenth Bird Report, 1988, The Cyprus Ornithological Society, Kailas Press, Nicosia, 1990.
Colomer, M. À., Margalida, A., Sanuy, D., and Pérez-Jiménez, M. J.: A bio-inspired computing model as a new tool for modeling ecosystems: The avian scavengers as a case study, Ecol. Model., 222, 33–47, https://doi.org/10.1016/j.ecolmodel.2010.09.012, 2011.
Colomer, M. À., Oliva-Vidal, P., Jiménez, J., Martínez, J. M., and Margalida, A.: Prioritizing among removal scenarios for the reintroduction of endangered species: insights from bearded vulture simulation modeling, Anim. Conserv., 23, 396–406, https://doi.org/10.1111/acv.12549, 2020.
Deredec, A. and Courchamp, F.: Importance of the Allee effect for reintroductions, Ecoscience, 14, 440–451, https://doi.org/10.2980/1195-6860(2007)14[440:IOTAEF]2.0.CO;2, 2007.
DeVault, T. L., Rhodes, O. E., and Shivik, J. A.: Scavenging by vertebrates: Behavioral, ecological, and evolutionary perspectives on an important energy transfer pathway in terrestrial ecosystems, Oikos, 102, 225–234, https://doi.org/10.1034/j.1600-0706.2003.12378.x, 2003.
DeVault, T. L., Beasley, J. C., Olson, Z. H., Moleón, M., Carrete, M., Margalida, A., and Antonio, J.: Ecosystem services provided by avian scavengers, in: Why birds matter: Avian ecological function and ecosystem services, edited by: Şekercioğlu, Ç. H., Wenny, D. G., and Whelan, C. J., University of Chicago Press, Chicago, USA, 235–270, 2016.
Duriez, O., Herman, S., and Sarrazin, F.: Intra-specific competition in foraging Griffon Vultures Gyps fulvus: 2. The influence of supplementary feeding management, Bird Study, 59, 193–206, https://doi.org/10.1080/00063657.2012.658640, 2012.
Fagan, W. F., Meir, E., Prendergast, J., Ayoola, F., and Kareiva, P.: Characterizing population vulnerability for 758 species, Ecol. Lett., 4, 132–138, https://doi.org/10.1046/j.1461-0248.2001.00206.x, 2001.
Flather, C. H., Hayward, G. D., Beissinger, S. R., and Stephens, P. A.: Minimum viable populations: is there a 'magic number' for conservation practitioners?, Trends Ecol. Evol., 26, 307–316, https://doi.org/10.1016/j.tree.2011.03.001, 2011.
Frankham, R.: Inbreeding and Extinction: A Threshold Effect, Conserv. Biol., 9, 792–799, https://doi.org/10.1046/j.1523-1739.1995.09040792.x, 1995.
Gil-Sánchez, J. M., Aguilera-Alcalá, N., Moleón, M., Sebastián-González, E., Margalida, A., Morales-Reyes, Z., Durá-Alemañ, C. J., Oliva-Vidal, P., Pérez-García, J. M., and Sánchez-Zapata, J. A.: Biases in the Detection of Intentionally Poisoned Animals: Public Health and Conservation Implications from a Field Experiment, Int. J. Env. Res. Pub. He., 18, 1201, https://doi.org/10.3390/ijerph18031201, 2021.
Griffith, B., Scott, M. J., Carpenter, J. W., and Reed, C.: Translocation as a Species Conservation Tool: Status and Strategy, Science, 245, 477–480, https://doi.org/10.1126/science.245.4917.477, 1989.
Grimm, V. and Railsback, S. F.: Individual-based Modelling and Ecology, Princeton University Press, Princeton and Oxford, UK, 2005.
Grimm, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., Goss-Custard, J., Grand, T., Heinz, S., K., Huse, G., Huth, A., Jepsen, J. U., Jørgensen, C., Mooij, W. M., Müller, B., Pe'er, G., Piou, C., Railsback, S. F., Robbins, A. M., Robbins, M. M., Rossmanith, E., Rüger, N., Strand, E., Souissi, S., Stillman, R. A., Vabø, R., Visser, U., and DeAngelis, D. L.: A standard protocol for describing individual-based and agent-based models, Ecol. Model., 198, 115–126, https://doi.org/10.1016/j.ecolmodel.2006.04.023, 2006.
Grussu, M. and Sardinian Ornithological Group: Evolution of the vulture population on a Mediterranean island. The Sardinian instance (Italy), Vulture News, 76, 6–19, https://doi.org/10.4314/vulnew.v76i1.2, 2019.
Halley, J. M.: Poison Baits and Vultures, OSF, available at: https://osf.io/tnvuh/?view_only=205bcf1f4a274c579591454827023b79, last access: 18 September 2019.
Halley, J. M. and Hoelzel, A. R.: Simulation Models of Bottleneck Events in Natural Populations, in: Molecular Genetic Approaches in Conservation, edited by: Smith, T. B. and Wayne, R. K., Oxford University Press, New York, UK, 1996.
Henriquez, M., Buij, R., Monteiro, H., Sá, J., Wambar, F., Tavares, J. P., Botha, A., Citegetse, G., Lecoq, M., Catry, P., and Ogada, D.: Deliberate poisoning of Africa's vultures, Science, 16, 304, https://doi.org/10.1126/science.abd1862, 2020.
Hernández, M. and Margalida, A.: Pesticide abuse in Europe: effects on the Cinereous vulture (Aegypius monachus) population in Spain, Ecotoxicology, 17, 264–272, https://doi.org/10.1007/s10646-008-0193-1, 2008.
Hernández, M. and Margalida, A.: Poison-related mortality effects in the endangered Egyptian vulture (Neophron percnopterus) population in Spain, Eur. J. Wildlife Res., 55, 415–423, https://doi.org/10.1007/s10344-009-0255-6, 2009.
Hoelzel, A. R., Halley, J. M., O'Brien, S. J., Campagna, C., Arnbom, T., Leboeuf, B., Ralls, K., and Dover, G. A.: Elephant seal genetic-variation and the use of simulation-models to investigate historical population bottlenecks, J. Hered., 84, 443–449, https://doi.org/10.1093/oxfordjournals.jhered.a111370, 1993.
Houston, D. C.: Reintroduction programmes for vulture species, in: Proceedings of the International Conference on Conservation and Management of Vulture Populations, edited by: Houston, D. C. and Piper, S. E., Natural History Museum of Crete and WWF Hellas, Thessaloniki, Greece, 14–16 November 2005, 87–97, 2006.
Iezekiel, S., Bakaloudis, D. E., and Vlachos, C. G.: The Status and Conservation of Griffon Vulture Gyps fulvus in Cyprus, in: Raptors worldwide: Proceedings of the VI World Conference on Birds of Prey and Owls, edited by: Meyburg, B.-U. and Chancellor, R., WWGBP and MME, Budapest, Hungary, 18–23 May 2003, 67–73, 2004.
IUCN Bangladesh: Vultures and Vulture Safe Zones of Bangladesh, IUCN, Bangladesh Country Office, Dhaka, Bangladesh, 51–151, 2016.
IUCN/SSC: Guidelines for Reintroductions and Other Conservation Translocations. Version 1.0, IUCN Species Survival Commission, viiii, Gland, Switzerland, 2013.
Kane, A., Jackson, A. L., Ogada, D. L., Monadjem, A., and McNally, L.: Vultures acquire information on carcass location from scavenging eagles, P. Roy. Soc. B-Biol. Sci., 281, 20141072, https://doi.org/10.1098/rspb.2014.1072, 2014.
Kassinis, N., Papazoglou, C., Xirouchakis, S., Probonas, M., and Papadopoulos, M.: Conservation of the declining Griffon Vulture Gyps fulvus population in Cyprus through reinforcement with individuals from Crete, in: Abstracts of the International Congress on the Zoogeography and Ecology of Greece and Adjacent Regions, edited by: Poulakakis, N., Antoniou, A., Karameta, E., Psonis, N., and Vardinoyannis, K., 13th ICZEGAR, Hellenic Zoological Society, 7–11 October 2015, Irakleio, Crete, Greece, 2015.
Kassinis, N., Apostolidou, M., and Ieronymidou, C.: Griffon Vultures of Cyprus – legacy of conservation past and looking to the future, in: Book of Abstracts, The European Vulture Conference, Algarve, Portugal, 1–3 October 2019, 61, 2019.
Knowlton, J. L. and Graham, C. H.: Using behavioral landscape ecology to predict species' responses to land-use and climate change, Biol. Conserv., 143, 1342–1354, https://doi.org/10.1016/j.biocon.2010.03.011, 2010.
Lacy, R. C. and Pollak, J. P.: Vortex: a stochastic simulation of the extinction process, version 10.0, Chicago Zoological Society, Brookfield, Illinois, USA, available at: https://scti.tools/, last access: 15 May 2014.
Le Gouar, P., Rigal, F., Boisselier-Dubayle, M. C., Sarrazin, F., Arthur, C., Choisy, J. P., Hatzofe, O., Henriquet, S., Lécuyer, P., Tessier, C., Susic, G., and Samadi, S.: Genetic variation in a network of natural and reintroduced populations of Griffon Vulture (Gyps fulvus) in Europe, Conserv. Genet., 9, 349–359, https://doi.org/10.1007/s10592-007-9347-6, 2008.
Lomnicki, A.: Individual-based Models in Population Ecology, eLS, https://doi.org/10.1002/9780470015902.a0003312.pub2, 2011.
Margalida, A.: Baits, budget cuts: a deadly mix, Science, 338, 192, https://doi.org/10.1126/science.338.6104.192-a, 2012.
Margalida, A. and Mateo, R.: Illegal killing of birds in Europe continues, Science, 363, 1161, https://doi.org/10.1126/science.aaw7516, 2019.
Margalida, A., Oliva-Vidal, P., Llamas, A., and Colomer, M. À.: Bioinspired models for assessing the importance of transhumance and transboundary management in the conservation of European avian scavengers, Biol. Conserv., 228, 321–330, https://doi.org/10.1016/j.biocon.2018.11.004, 2018.
Markandya, A., Taylor, T., Longo, A., Murty, M. N., and Dhavala, K.: Counting the Cost of Vulture Declines – Economic Appraisal of the Benefits of the Gyps Vulture in India, Ecol. Econ., 67, 194–204, https://doi.org/10.1016/j.ecolecon.2008.04.020, 2008.
Mateo-Tomás, P. and Olea, P. P.: Anticipating knowledge to inform species management: Predicting spatially explicit habitat suitability of a colonial vulture spreading its range, PLoS ONE, 5, e12374, https://doi.org/10.1371/journal.pone.0012374, 2010.
McClure, C. J. W., Westrip, J. R. S., Johnson, J. A., Schulwitz, S. E., Virani, M. Z., Davies, R., Symes, A., Wheatley, H., Thorstrom, R., Amar, A., Buij, R., Jones, V. R., Williams, N. P., Buechley, E. R., and Butchart, S. H. M.: State of the world's raptors: Distributions, threats, and conservation recommendations, Biol. Conserv., 227, 390–402, https://doi.org/10.1016/j.biocon.2018.08.012, 2018.
McGowan, C. P., Runge, M. C., and Larson, M. A.: Incorporating parametric uncertainty into population viability analysis models, Biol. Conserv., 5, 1400–1408, https://doi.org/10.1016/j.biocon.2011.01.005, 2011.
Mereu, P., Satta, V., Frongia, G. N., Berlinguer, F., Muzzeddu, M., Campus, A., Decandia, L., Pirastru, M., Manca, L., Naitana, S., and Leoni, G. G.: The complete mtDNA sequence of the Griffon Vulture (Gyps fulvus): Phylogenetic analysis and haplotype frequency variations after restocking in the Sardinian population, Biol. Conserv., 214, 195–205, https://doi.org/10.1016/j.biocon.2017.08.017, 2017.
Mihoub, J.-B., Robert, A., Le Gouar, P., and Sarrazin, F.: Post-release dispersal in animal translocations: Social attraction and the “Vacuum Effect”, PLoS ONE, 6, e27453, https://doi.org/10.1371/journal.pone.0027453, 2011.
Moleón, M. and Sánchez-Zapata, J. A.: The Living Dead: Time to Integrate Scavenging into Ecological Teaching, BioScience, 65, 1003–1010, https://doi.org/10.1093/biosci/biv101, 2015.
Moleón, M., Sánchez-Zapata, J. A., Margalida, A., Carrete, M., Owen-Smith, N., and Donázar, J. A.: Humans and Scavengers: The Evolution of Interactions and Ecosystem Services, BioScience, 64, 394–403, https://doi.org/10.1093/biosci/biu034, 2014.
Monsarrat, S., Benhamou, S., Sarrazin, F., Bessa-Gomes, C., Bouten, W., and Duriez, O.: How Predictability of Feeding Patches Affects Home Range and Foraging Habitat Selection in Avian Social Scavengers?, PLoS ONE, 8, e53077, https://doi.org/10.1371/journal.pone.0053077, 2013.
Morales-Reyes, Z., Pérez-García, J. M., Moleón, M., Botella, F., Carrete, M., Lazcano, C., Moreno-Opo, R., Margalida, A., Donázar, J. A., and Sánchez-Zapata, J. A.: Supplanting ecosystem services provided by scavengers raises greenhouse gas emissions, Sci. Rep.-UK, 5, 7811, https://doi.org/10.1038/srep07811, 2015.
Moreno-Opo, R., Trujillano, A., and Margalida, A.: Optimization of supplementary feeding programs for European vultures depends on environmental and management factors, Ecosphere, 6, 127, https://doi.org/10.1890/ES15-00009.1, 2015.
Murn, C. and Botha, A.: A clear and present danger: impacts of poisoning on a vulture population and the effect of poison response activities, Oryx, 52, 552–558, https://doi.org/10.1017/S0030605316001137, 2018.
Ntemiri, K., Saravia, V., Angelidis, C., Baxevani, K., Probonas, M., Kret, E., Mertzanis, Y., Iliopoulos, Y., Georgiadis, L., Skartsi, D., and Vavylis, D.: Animal mortality and illegal poison bait use in Greece, Environ. Monit. Assess., 190, 488, https://doi.org/10.1007/s10661-018-6838-5, 2018.
Oaks, J. L., Gilbert, M., Virani, M. Z., Watson, R. T., Meteyer, C. U., Rideout, B. A., Shivaprasad, H. L., Ahmed, S., Chaudhry, M. J., Arshad, M., Mahmood, S., Ali, A., and Khan, A. A.: Diclofenac residues as the cause of vulture population decline in Pakistan, Nature, 427, 630–633, https://doi.org/10.1038/nature02317, 2004.
Ogada, D., Shaw, P., Beyers, R. L., Buij, R., Murn, C., Thiollay, J. M., Beale, C. M., Holdo, R. M., Pomeroy, D., Baker, N., Krüger, S. C., Botha, A., Virani, M. Z., Monadjem, A., and Sincliair, A. R. E.: Another Continental Vulture Crisis: Africa's Vultures Collapsing toward Extinction, Conserv. Lett., 9, 89–97, https://doi.org/10.1111/conl.12182, 2015.
Ogada, D., Botha, A., and Shaw, P.: Ivory Poachers and Poison: Drivers of Africa's Declining Vulture Populations, Oryx, 50, 593–596, https://doi.org/10.1017/S0030605315001209, 2016.
Ogada, D. L.: Power of Poison: Pesticide Poisoning of Africa's wildlife, Ann. N.Y. Acad. Sci., 1322, 1–20, https://doi.org/10.1111/nyas.12405, 2014.
Ogada, D. L., Keesing, F., and Virani, M. Z.: Dropping dead: Causes and consequences of vulture population declines worldwide, Ann. N.Y. Acad. Sci., 1249, 57–71, https://doi.org/10.1111/j.1749-6632.2011.06293.x, 2011.
Ogada, D. L., Torchin, M. E., Kinnaird, M. F., and Ezenwa, V. O.: Effects of Vulture Declines on Facultative Scavengers and Potential Implications for Mammalian Disease Transmission, Conserv. Biol., 26, 453–460, https://doi.org/10.1111/j.1523-1739.2012.01827.x, 2012.
Pain, D. J., Cunningham, A. A., Donald, P. F., Duckworth, J. W., Houston, D. C., Katzner, T., Parry-Jones, J., Poole, C., Prakash, V., Round, P., and Timmins, R.: Causes and Effects of Temporo spatial Declines of Gyps Vultures in Asia, Conserv. Biol., 17, 661–671, https://doi.org/10.1046/j.1523-1739.2003.01740.x, 2003.
Panagiotopoulou, M., Azmanis, P., Tsiakiris, R., and Stara, K.: Carry on Carrion: the fall of the Scavenger, in: Animal Welfare in a Changing World, edited by: Butterworth, A., CABI, Oxfordshire, UK, 57–67, https://doi.org/10.1079/9781786392459.0057, 2018.
Parvanov, D. E., Stoynov, N., Vangelova, H., Peshev, A., Grozdanov, V., Delov, V., and Iliev, Y.: Vulture mortality resulting from illegal poisoning in the southern Balkan Peninsula, Environ. Sci. Pollut. R., 25, 1706–1712, https://doi.org/10.1007/s11356-017-0594-x, 2018.
Peshev, H., Grozdanov, A., Kmetova-Biro, E., Ivanov, I., Stoyanov, G., Tsiakiris, R., Marin, S., Marinković, S., Sušić, G., Lisichanets, E., Hribšek, I., Karić, Z., Kapelj, S., Bonchev, L., and Stoynov, E.: New insight into spatial ecology of Griffon Vulture (Gyps fulvus) on the Balkans provides opportunity for focusing conservation actions for a threatened social scavenger, Biodiversity Data Journal, 9, e71100, https://doi.org/10.3897/BDJ.9.e71100, 2021.
Piper, S. E.: Supplementary feeding programmes: how necessary are they for the maintenance of numerous and healthy vulture populations, in: Proceedings of the International Conference on Conservation and Management of Vulture Populations, edited by: Houston, D. C. and Piper, S. E., Natural History Museum of Crete and WWF Hellas, Thessaloniki, Greece, 14–16 November 2005, 41–50, 2006.
Prakash, V., Pain, D. J., Cunningham, A. A., Donald, P. F., Prakash, N., Verma, A., Gargi, R., Sivakumar, S., and Rahmani, A. R.: Catastrophic collapse of Indian white-backed Gyps bengalensis and long billed Gyps indicus vulture populations, Biol. Conserv., 109, 381–390, https://doi.org/10.1016/S0006-3207(02)00164-7, 2003.
Ruxton, G. D. and Houston, D. C.: Obligate vertebrate scavengers must be large soaring fliers, J. Theor. Biol., 228, 431–436, https://doi.org/10.1016/j.jtbi.2004.02.005, 2004.
Safford, R., Andevsky, J., Botha, A., Bowden, C. G. R., Crockford, N., Garbett, R., Margalida, A., Ramírez, I., Shobrak, M., Tavares, J., and Williams, N. P.: Vulture Conservation: the Case for Urgent Action, Bird Conserv. Int., 29, 1–9, https://doi.org/10.1017/S0959270919000042, 2019.
Sarrazin, F.: Introductory remarks. A demographic frame for reintroductions, Ecoscience, 14, 4, https://doi.org/10.2980/1195-6860(2007)14[iii:RL]2.0.CO;2, 2007.
Sarrazin, F. and Legendre, S.: Demographic Approach to Releasing Adults versus Young in Reintroductions, Conserv. Biol., 14, 488–500, https://doi.org/10.1046/j.1523-1739.2000.97305.x, 2000.
Sarrazin, F., Bagnoline, C., Pinna, J. L., and Danchin, E.: Breeding biology during establishment of a reintroduced Griffon Vulture Gyps fulvus population, Ibis, 138, 315–325, https://doi.org/10.1111/j.1474-919X.1996.tb04344.x, 1996.
Şekercioğlu, Ì. H., Daily, G. C., and Ehrlich, P. R.: Ecosystem consequences of bird declines, P. Natl. Acad. Sci. USA, 101, 18042–18047, https://doi.org/10.1073/pnas.0408049101, 2004.
Shaffer, M.: Minimum viable populations: coping with uncertainty, in: Viable Populations for Conservation, edited by: Soulé, M. E., Cambridge University Press, Cambridge, UK, 69–86, https://doi.org/10.1017/CBO9780511623400.006, 1987.
Smith, D.: Africa's vulture population in jeopardy following mass poisoning incidents, The Guardian, 2 June 2014, available at: https://www.theguardian.com/world/2014/jun/26/vultures-africa-poison-carcasses-poachers-crisis, last access: 26 February 2021.
Soulé, M. E.: Diversity, Conserv. Biol., 1, 173–174, https://doi.org/10.1111/j.1523-1739.1987.tb00027.x, 1987.
Stavrinides, M.: Reinforcement of Vultures in Cyprus Material-Methods and First Results, in: Book of Abstracts of the International Workshop on “The Future of Vultures in Balkans: Tackling Threats and Building Network Opportunities”, edited by: Tsiakiris, R. and Pergantis, F., Messolongi, Greece, 7–9 December 2018, 38, 2019.
Stoev, I., Bonchev, L., Stoynov, E., Kmetova-Biro, E., Ivanov, I., Yankov, L., Iliev, Y., Nikolova, Z., and Vangelova, N.: Restoration of Griffon Vulture (Gyps fulvus) in eastern Balkan Mountains, Bulgaria, in: Annuaire de l' Université de Sofia “St. Kliment Ohridski”, Faculté de Biologie, Presses Universitaires “St. Kliment Ohridski”, Sofia, Bulgaria, 116–129, 2016.
Stoynov, E., Peshev, H., Grozdanov, A., and Vangelova, N.: Reintroduction of the Griffon Vulture (Gyps fulvus) in Kresna gorge, south-west Bulgaria in the period 2010–2015, in: Annuaire de l' Université de Sofia “St. Kliment Ohridski”, Faculté de Biologie, Presses Universitaires “St. Kliment Ohridski”, Sofia, Bulgaria, 130–135, 2016.
Stoynov, E., Vangelova, N., Zlatanova, D., Peshev, H., Parvanov, D., Delov, V., and Grozdanov, A.: Wolf and Vultures Sympatric Presence in Europe: Ecological Benefits and Constraints, Acta Zool. Bulgar., Suppl. 12, 85–92, 2018.
Stoynov, E., Peshev, H., Parvanov, D., and Grozdanov, A.: Breakthrough in Anti-poison Struggle after Introduction of Intensive Satellite Tracking of Griffon Vultures in Balkans, ECOLOGIA BALKANICA, Special Edition, 2, 15–21, 2019.
Terrasse, M., Sarrazin, F., Choisy, J.-P., Clémente, C., Henriquet, S., Lécuyer, P., Pinna, J.-L., and Tessier, C.: A success story: the reintroduction of Eurasian Griffon Gyps fulvus and Black Aegypius monachus vultures to France, in: Raptors worldwide: proceedings of the VI World Conference on Birds of Prey and Owls, edited by: Meyburg, B.-U. and Chancellor, R., WWGBP and MME, Budapest, Hungary, 18–23 May 2003, 127–145, 2004.
Van Houtan, K. S., Bass Jr., O. L., Lockwood, J., and Pimm, S. L.: Importance of estimating dispersal for endangered bird management, Conserv. Lett., 3, 260–266, https://doi.org/10.1111/j.1755-263X.2010.00108.x, 2010.
Van Overveld, T., García-Alfonso, M., Dingemanse, N. J., Bouten, W., Gangoso, L., de la Riva, M., Serrano, D., and Donázar, J. A.: Food predictability and social status drive individual resource specializations in a territorial vulture, Sci. Rep.-UK, 8, 1–13, https://doi.org/10.1038/s41598-018-33564-y, 2018.
Van Overveld, T., Blanco, G., Moleón, M., Margalida, A., Sánchez-Zapata, J. A., de la Riva, M., and Donázar, J. A.: Integrating vulture social behavior into conservation practice, Ornithological Applications, 122, 1–20, https://doi.org/10.1093/condor/duaa035, 2020.
Vasilakis, D. P., Whitfield, D. P., Schindler, S., Poirazidis, K. S., and Kati, V.: Reconciling endangered species conservation with wind farm development: Cinereous vultures in south-eastern Europe, Biol. Conserv., 196, 10–17, https://doi.org/10.1016/j.biocon.2016.01.014, 2016.
Velevski, V., Nikolov, S. C., Hallman, B., Dobrev, V., Sidiropoulos, L., Saravia, V., Tsiakiris, R., Arkumarev, V., Galanaki, A., Kominos, T., Stara, K., Kret, E., Grubač, B., Lisičanec, E., Kastritis, T., Vavylis, D., Topi, M., Hoxha, B., and Oppel, S.: Population decline and range contraction of the Egyptian Vulture Neophron percnopterus in the Balkan Peninsula, Bird Conserv. Int., 25, 440–450, https://doi.org/10.1017/S0959270914000343, 2015.
Whitfield, D. P., Fielding, A. H., MacLeod, D. R. A., and Haworth, P. F.: The effects of persecution on age of breeding and territory occupation in golden eagles in Scotland, Biol. Conserv., 118, 249–259, https://doi.org/10.1016/j.biocon.2003.09.003, 2004.
Wilson, A. C. and Stanley Price, M. R.: Reintroduction as a reason for captive breeding, in: Creative Conservation, edited by: Olney, P. J. S., Mace, G. M., and Feistner, A. T. C., Springer, Dordrecht, Holland, 243–264, https://doi.org/10.1007/978-94-011-0721-1_12, 1994.
Wilson, E. E. and Wolkovich, E. M.: Scavenging: How carnivores and carrion structure communities, Trends Ecol. Evol., 26, 129–135, https://doi.org/10.1016/j.tree.2010.12.011, 2011.
Xirouchakis, S.: The ecology of the Eurasian Griffon Vulture (Gyps fulvus) on the island of Crete, PhD thesis, University of Crete, Crete, 412 pp., 2002.
Xirouchakis, S.: Breeding biology and reproductive performance of Griffon Vultures Gyps fulvus on the island of Crete, Bird Study, 57, 213–225, https://doi.org/10.1080/00063650903505754, 2010.
Xirouchakis, S., Andreou, G., and Arnellos, G.: The impact of poisoned baits set for vermin on the population of vultures in Crete (Greece). Incidences of secondary poisoning during 1990–1999, Vulture News, 42, 13–24, 2000.
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Appendix A: Description of mathematical model for the griffon vulture population
- Appendix B: Framework describing simulation model
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Methods
- Results
- Discussion
- Appendix A: Description of mathematical model for the griffon vulture population
- Appendix B: Framework describing simulation model
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References





