Perlin noise as a hierarchical neutral landscape model

Neutral landscape models based on fractal algorithms are used widely by landscape ecologists. Perlin noise is a spectral synthesis algorithm that has not been widely adopted by landscape ecologists, even though the hierarchical properties of Perlin noise are particularly relevant to landscape ecology. To encourage the use of Perlin noise, I provide an explanation of the algorithm in the context of neutral landscape models to demonstrate that the hierarchical nature of the algorithm not only allows for a wide range of possible spatial patterns to be produced, but also usefully parallels theories about the hierarchical structure of landscapes.

1 Introduction

Neutral landscape models are a key concept and technique in landscape ecology that allow researchers to explore the influence of landscape pattern and structure on ecological processes and methods. Conducting landscape-scale experiments in the real world is logistically challenging or even impossible, and the uniqueness of any landscape limits the value of experimental replication (Turner and Gardner, 2015; Wang and Malanson, 2008). In contrast to real-world experimentation, by using a computer to simulate many landscapes with varying but highly controlled spatial patterns, landscape ecologists can create an experimental baseline with which to evaluate the effect of ecological processes on landscape pattern and conversely the effect of landscape pattern on ecological processes (With and King, 1997). For example, neutral landscape models have been used to explore how changes in the abundance and distribution of habitat within a landscape may affect a species' distribution, abundance, dispersal, and ultimately survival within a landscape with applications to the conservation of threatened species and the control of invasive species (for an extended list of neutral landscape model applications, see Wang and Malanson, 2008).

The simplest neutral landscape model is a grid within which each cell has a specified probability of being habitat, and even these simple models provide interesting insights into critical thresholds associated with landscape connectivity (Gardner et al., 1987). However, more realistic neutral landscape models that mimic the spatial patterns of real landscapes have been developed using methods originating from fractal geometry (Mandelbrot, 1983). A hierarchal fractal neutral landscape model can be created via random curds and implements a process of spatial subdivision where the landscape is repeatedly subdivided by probabilities specific to each hierarchical level to create a landscape in which habitat is more clustered (O'Neill et al., 1992). Another fractal neutral landscape model is based on two-dimensional Brownian motion that uses a parameter that controls the randomness of the motion to produce neutral landscape models with a gradient that can range from highly clustered to highly fragmented (Palmer, 1992). These simple and fractal neutral landscape models are the methods most commonly used by landscape ecologists (Wang and Malanson, 2008). An alternative approach to neutral landscape models is one based on spectral (or sound, noise) synthesis in which $\mathrm{1}/f$ noise, wavelets, and Fourier transforms are applied in two dimensions to produce potentially complex landscape patterns from a hierarchy of spatial gradients (Keitt, 2000). In essence, spectral synthesis works by combining a series of waves of increasing frequency and decreasing amplitude to produce an overall pattern that combines the desirable hierarchal and variable spatial gradient properties of the commonly used fractal neutral landscape models.

Although spectral synthesis methods have much potential for neutral landscape models (Keitt, 2000), they have not been widely adopted by landscape ecologists (Wang and Malanson, 2008). This is in notable contrast to the field of computer graphics, where the creation of neutral landscape models, or virtual worlds, has an even longer history. In computer graphics fractal algorithms such as the mid-point displacement method (Fournier et al., 1982) that was later adopted by landscape ecologists (Palmer, 1992) was actually developed to produce science fiction classics such as “Star Trek II: The Wrath of Khan” (Falconer, 2013). The successful application of fractals in computer graphics has resulted in a large range of procedural modelling algorithms (Smelik et al., 2014) that are ubiquitous in the production of movies and computer games, but perhaps because of differences in terminology these procedural modelling algorithms have not been exploited by landscape ecologists. A prime example of this situation is that of Perlin noise that was originally developed to mimic the appearance of things such as water, marble, and fire (Perlin, 1985) but that was later used to mimic the terrain of a landscape (Musgrave et al., 1989) and is now a primary method used in computer graphics for creating virtual worlds (Smelik et al., 2014). Perlin noise is a form of spectral synthesis that sits within the $\mathrm{1}/f$ family of noises (Parberry, 2014; Musgrave et al., 1989), and as spectral synthesis has been shown to be relevant to neutral landscape modelling (Keitt, 2000), Perlin noise should also be useful as a neutral landscape model. Indeed, Perlin noise has been used as a neutral landscape model (Smets et al., 2019; Lavorel et al., 2022), but very rarely, perhaps because the algorithm and its relevance to landscape ecology have not been explained. Therefore, I aim to explain Perlin noise in a way that will be intuitive to ecologists, demonstrate how Perlin noise can be used to produce a wide range of useful neutral landscape models, and relate Perlin noise to theories about the hierarchical structure of landscapes.

2 Perlin noise

Perlin noise, as the name indicates, uses terminology from the physics of sound to define its four parameters: periods, lacunarity, persistence, and octaves. As this terminology may be unfamiliar to landscape ecologists, and as some of the terms can have different meanings in other fields of study, I will begin by introducing the terminology of Perlin noise using a simple example of generating a sound wave from a set of sine waves. A sine wave in its basic form without any vertical shifts consists of a series of wave periods that each cycle between a start and end value of zero. For Perlin noise the periods parameter determines the number of waves generated, and increasing the number of periods within the same spatial distance increases the spatial frequency of the wave. The amplitude is a measure of the magnitude or strength of a wave determined by how much a wave changes from zero over a single period. By simply varying the number of periods and the amplitude, a variety of different sine waves can be created (Fig. 1a to c), the summation of which produces a sound wave (Fig. 1d).

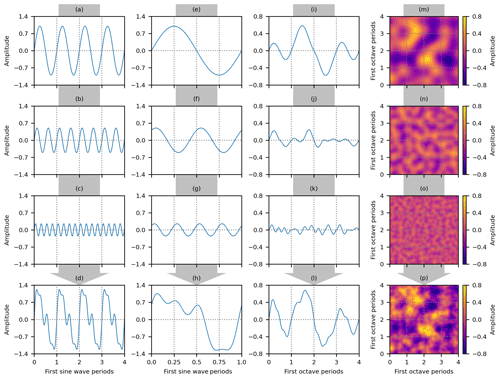
Figure 1 Example construction of one-dimensional sound and noise waves from sine waves and one- and two-dimensional Perlin noise. A series of sine waves with (a) periods = 4 and amplitude = 1, (b) periods = 8 and amplitude = 0.5, and (c) periods = 16 and amplitude = 0.25, the summation of which produces (d) a sound wave where $d=a+b+c$. A series of out-of-phase sine waves with (e) periods = 1 and amplitude = 1, (f) periods = 2 and amplitude = 0.5, and (g) periods = 4 and amplitude = 0.25, the summation of which produces (h) a noise wave where $h=e+f+g$. A series of Perlin noise waves, called octaves, with periods = 4 and amplitude ≤ 1 in (i) one dimension and (m) two dimensions, periods = 8 and amplitude ≤ 0.5 in (j) one dimension and (n) two dimensions, and periods = 16 and amplitude ≤ 0.25 in (k) one dimension and (o) two dimensions, the summation of which produces Perlin noise in (l) one dimension where $l=i+j+k$ and (p) two dimensions where $p=m+n+o$. In all cases the lacunarity = 2 as the number of periods (or spatial frequency) doubles, and persistence = 0.5 as the amplitude halves.

Having shown how a sound wave can be generated from a series of sine waves, other terms of importance specific to Perlin noise can be defined. Lacunarity is a measure of how fractal patterns fill space (Falconer, 2013), and in the context of Perlin noise the lacunarity parameter is a multiplier that determines the rate of change in the number of periods between successive waves. For example, when lacunarity = 2, then the number of periods doubles for each successive wave (Fig. 1a to c), or when lacunarity = 4, then the number of periods quadruples for each successive wave. The persistence parameter is a multiplier that determines the rate at which the amplitude decreases between successive waves. For example, when persistence = 0.5, then the amplitude halves for each successive wave (Fig. 1a to c), or when persistence = 0.25, then the amplitude quarters for each successive wave.

The link between sound waves and neutral landscape models may not be immediately evident. However, the series of sine waves are a hierarchical set of patterns, and such hierarchical patterns can be useful when creating neutral landscape models (Wang and Malanson, 2008). Therefore, if the frequency of each sine wave represents the spatial scale of each landscape feature in terms of how often it occurs and the amplitude of each sine wave represents the magnitude of each landscape feature in terms of the size of the effect, then the summation of the sine waves into a sound wave can produce a pattern that can be used as the basis of a neutral landscape model (Keitt, 2000). For example, mountain ranges would be a low-frequency, high-amplitude landscape feature as the low frequency means there are few mountain ranges per landscape and the high amplitude that the effect of each mountain range on landscape pattern is large. Conversely, the occurrence of a particular tree species could be a high-frequency, low-amplitude landscape feature as the occurrence of the species could be highly variable across a landscape and the presence of the species may have a small effect on the overall landscape pattern. The cyclical nature of sine waves produces a sound wave that has a repetitive pattern unlikely to be found in real landscapes (Fig. 1d), so to produce realistic neutral landscape models, a method to produce irregular or noisy sound waves is required. For spectral synthesis methods such as wavelets and Fourier transforms, in essence these noisy waves are achieved by the summation of sine or cosine waves that are out of phase, meaning that the locations of the ends of wave periods do not intersect and that they have randomised rather than systematic changes in frequency and amplitude (Keitt, 2000; Chipperfield et al., 2011). This process will usually involve many sine or cosine waves, but a very simple example of three out-of-phase sine waves of increasing frequency and deceasing amplitude (Fig. 1e to g) is sufficient to demonstrate the principle that the summation of regular sine waves can produce a noisy wave with an irregular pattern that is more likely to be found in real landscapes (Fig. 1h).

An alternative approach to combining regular sine or cosine waves to produce irregular noise is to create a gradient (or coherent) noise that is smooth like a sine wave but in contrast is immediately irregular and is stochastic so that an unlimited number of different possible noises can be produced from the same input parameters. A widely used example of gradient noise is Perlin noise (Perlin, 1985) that, very briefly, is not created from the summation of sine or cosine waves but instead is created by generating random gradient values at the locations at the ends of wave periods and then interpolating the gradient values between these locations to immediately create a smooth noise wave (Parberry, 2014; Lagae et al., 2010). Perlin noise waves are like sine waves in that they also have a regular period with the wave starting and ending each period at zero – though unlike a sine wave a Perlin noise wave is not guaranteed to cross zero during the period cycle (Fig. 1i). As with the sine waves, by specifying a lacunarity and persistence, a series of Perlin noise waves can be produced that have an ever-increasing number of periods and ever-decreasing amplitude (Fig. 1i to k). In Perlin noise terminology each of these noise waves is called an octave, as the standard value of lacunarity = 2 results in a doubling of the periods and hence a doubling of the spatial frequency, which parallels a musical context where an octave is the interval between two notes with double the frequency. The octave parameter of Perlin noise determines the number of octaves that will form the Perlin noise. So, with octaves = 3 a series of three octaves is created (Fig. 1i to k), and the summation of these octaves that remain in phase with one another produces Perlin noise that has a very irregular pattern (Fig. 1l). Perlin noise can just as easily be applied in two dimensions using the same parameters. A hierarchical series of two-dimensional octaves with increasing periodicity and decreasing amplitude is created (Fig. 1m to o), the summation of which produces two-dimensional Perlin noise (Fig. 1p). When viewed in two dimensions the relevance of Perlin noise for neutral landscape modelling should be evident, as two-dimensional Perlin noise has a clear fractal pattern that is like that produced by the mid-point displacement method that has been used widely as a neutral landscape model.

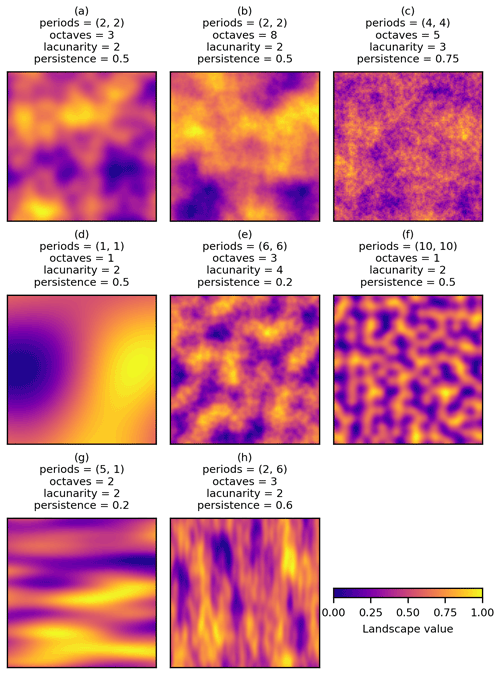
The Perlin noise parameters of number of periods (horizontal and vertical), number of octaves, lacunarity, and persistence can be changed to produce a wide range of spatial patterns. Rescaling the resulting Perlin noise to range from zero to one to be consistent with neutral landscape modelling software (Etherington et al., 2015) produces a wide array of different neutral landscape models (Fig. 2). The possibilities are essentially endless, so Perlin noise should be able to generate neutral landscape models that have spatial patterns that are relevant to a very wide range of landscape contexts.

Figure 2 Example neutral landscape models demonstrating the wide range of possibilities that can be produced by varying the Perlin noise parameters of number of periods (top to bottom, left to right), number of octaves, lacunarity, and persistence.

3 Discussion

The main advantage of Perlin noise over other fractal methods such as the mid-point displacement method comes from the hierarchical structure of Perlin noise. The hierarchical structure allows for a very wide range of spatial patterns (Fig. 2), but the hierarchical structure also links nicely to hierarchical perspectives of landscape patterns. Landscape patterns can be very usefully viewed in a hierarchical sense, with processes operating at different spatial scales combining to produce an overall landscape pattern. For example, geological processes acting at the macroscale may provide an initial dominant restriction to forest patterns; these forest patterns are then affected by disturbance events operating at a mesoscale before individual tree mortality affecting patterns at the microscale (Turner and Gardner, 2015; Urban et al., 1987). This hierarchy of landscape processes combining to produce landscape patterns has obvious parallels to the octaves of Perlin noise with increasing frequency and decreasing amplitude combining to produce a neutral landscape model (Fig. 1m to p).

A possible disadvantage of Perlin noise is that, like all procedural generation methods, specifying the appropriate set of parameters can be bewildering, especially when the parameters can interact in non-intuitive ways, so that successful application of procedural generation methods such as Perlin noise can require a lot of experimentation (Smelik et al., 2014). Another possible disadvantage is software availability, as the only dedicated neutral landscape modelling software package that includes Perlin noise is the Python NLMpy package (Etherington et al., 2015) that was used to generate the examples provided here. However, as Perlin noise has a long and successful history, code for Perlin noise will likely exist in a variety of programming languages, and hopefully this introduction to Perlin noise from an ecological perspective will facilitate the use and development of such code in a landscape ecological application.

Of course, Perlin noise is not the only form of spectral synthesis that could be used for neutral landscape modelling, and although the flexible nature of the technique means that a wide variety of neutral landscape models can be produced that could have wide application potential (Fig. 2), Perlin noise is by no means perfect. For example, a limitation of Perlin noise when used to simulate terrain is that it often produces isolated valleys (Parberry, 2014). This problem with Perlin noise can be addressed via further processing of the simulated terrain via erosion modelling (Musgrave et al., 1989) or basin filling (Lavorel et al., 2022), or other procedural modelling algorithms such as value noise could be used instead in combination with real-world elevation data to produce more realistic terrain (Parberry, 2014). Other forms of spectral synthesis that also sit within the general family of $\mathrm{1}/f$ noises such as wavelets and Fourier transforms that are relevant for neutral landscape models (Keitt, 2000) have also been used in computer graphics alongside a variety of other procedurally generated gradient noises (Lagae et al., 2010). However, it is noteworthy that while the potential of wavelets and Fourier transforms for neutral landscape models was noted decades ago (Keitt, 2000), these approaches have not been widely adopted by landscape ecologists. Similarly, within computer graphics, while the potential of wavelets and Fourier transforms has been noted for some time (Lagae et al., 2010), Perlin noise continues to be the foundation of computer graphics virtual world generation. This preference for Perlin noise within computer graphics for virtual world generation indicates that Perlin noise may provide advantages over these other forms of spectral synthesis for neutral landscape modelling, but further comparative exploration of these methods for neutral landscape modelling would be helpful. It is also worth noting that landscape ecologists may well find that there are other procedural modelling algorithms that could be adapted to produce neutral landscape models, so further exploration of this domain crossover between computer graphics and landscape ecology would be useful.